Qué son los números enteros
Los números naturales y enteros no son más que aquellos grupos numéricos que poseen la totalidad de los dígitos naturales, así como el cero y sus inversos negativos. El conjunto de números enteros está designado con la letra Z, la cual hace alusión a los dígitos. Cada uno de ellos se representa con una recta numérica, la cual tiene el cero en el medio, dígitos positivos en la derecha y los negativos en la izquierda, extendiéndose ambos hacia el infinito.
El término número entero nace del latín númerus e integer, cuyo significado hace alusión a las clasificaciones de los dígitos naturales, es decir, 1, 2, 3, 4 y abarcado a los dígitos racionales, dos números enteros consecutivos, entre otros.
Propiedades de los números enteros
Dentro de las propiedades de este conjunto de dígitos, está el hecho que todas las operaciones de multiplicación y adición, forman una estructura algebraica de anillo.
Los números enteros se encuentran representados por la letra Z y son completamente ordenados, además, se pueden conceptualizar de acuerdo a diversas nociones de distancia entre dos dígitos diferentes, aunque lo más usual es que sean igual al valor absoluto que radica en su diferencia.
Desde el principio de los tiempos, las personas han tenido la imperiosa necesidad de llevar cuentas, para eso, se crearon los números naturales, pero con el paso de los años, los individuos se dieron cuenta que esto no era suficiente para poder representar las cantidades que manejan, así como tampoco les era de ayuda en situaciones difíciles, por ejemplo, si querían comparar temperaturas, dividir montos, cambiarlos a fracciones, entre otros.
Es por este motivo que la importancia de estos dígitos radica en que brindan comparaciones de cantidades, son el fundamento de los demás dígitos y funcionan para llevar cuentas de forma eficiente. Las representaciones positivas y negativas de los dígitos permiten que las personas puedan conocer las diferentes cantidades en tiempo y espacio.
Números enteros positivos y negativos
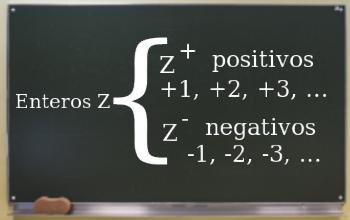
Los negativos son transcritos con el signo -, en los positivos no es necesario anexar el signo, sin embargo, se hace para dar a entender de cuál dígito se trata y se representa con el signo +. Los positivos enteros son mayores hacia la derecha, pero los negativos se vuelven más pequeños de acuerdo a los avances a la izquierda.
Números enteros pares e impares
Los pares son aquellos que se dividen en grupos de dos, por ejemplo, el cuatro, el cual puede dividirse y su resultado es dos. Los números impares no se pueden dividir de dos en dos, por ejemplo, el cinco se divide en dos grupos de dos y un grupo de uno. Los pares siempre van a terminar en dígitos como el 0, 2, 4, 6, 8. Los impares terminarán en dígitos como el 1, 3, 5, 7 y 9.
Operaciones con números enteros
Los números enteros son aquellos que pueden restarse, sumarse, dividirse y multiplicarse, claro está, siguiendo un modelo de dígitos naturales y agregando algunas normas para los usos de los signos. Es común asociar la suma de fracciones con números enteros y la división de fracciones con números enteros. A continuación se presenta una breve explicación de estas operaciones matemáticas:
Suma y resta de números enteros
Cuando se trata de sumar o restar números enteros se habla de la suma algebraica. Para ello es importante determinar por separado tanto el valor absoluto del resultado como el signo. Y aplicar la ley de los signos.
- Signos iguales se suman y se conserva el mismo signo: si los números cuentan con el mismo signo, entonces el resultado tendrá el mismo signo. El valor del resultado será la suma de los valores absolutos de los números, es decir, la suma de los números sin tomar en cuenta el signo.
- Signos diferentes se restan y se conserva el signo del mayor: cuando los sumandos (números que se están sumando) cuentan con distintos signos, entonces el signo del resultado tiene que corresponder con el de mayor valor absoluto. El valor absoluto del resultado es la diferencia entre el mayor y menor valor absoluto entre los dos sumandos.
Ejemplo:
a) +2 + 2 = +4
Donde, los sumandos 2 y 2 son ambos de signo positivo. El resultado es 4, la suma de los valores absolutos y el signo del resultado es +.
b) -3-8=-11
Donde, el sumando -3 tiene signo negativo y el sumando -8 también. Por ser signos iguales, se suman sus valores absolutos, es decir, 3 y 8, siendo el resultado 11. Este conserva el signo -.
Ejemplo:
a) +4 – 6 = -2
Donde, el sumando +4 tiene signo positivo y el sumando -6 tiene signo negativo. Por ser signos diferentes el resultado es la diferencia entre 6 y 4, que es 2. El signo del resultado corresponde con el signo del mayor valor, el cual es -.
b) 6 – 4 = 2
Donde, el sumando 6 tiene signo positivo y el sumando 4 tiene signo negativo. Por ser diferentes, el resultado será la diferencia de los valores absolutos. Esto corresponde con el número 2. El signo del resultado será + dado que el mayor valor absoluto de los sumandos tiene signo positivo.
Nota: El signo positivo + se puede omitir si antes del número positivo no hay ningún número.
En la siguiente tabla se puede observar las reglas a seguir para la suma y resta de números enteros.
del mayor |
||
del mayor |
||
Multiplicación y división de números enteros
En la multiplicación y división de los números enteros, es necesario determinar los signos y el valor absoluto del resultado por separado.
En este tipo de operaciones se debe aplicar la regla de los signos para la multiplicación y la división.
Para la multiplicación, el resultado se denomina producto, mientras que los números que se multiplican se llaman factores.
- Si ambos factores tienen el mismo signo, el resultado o producto tendrá signo positivo. Para obtenerlo se deben sumar uno de los factores tantas veces sean el valor del segundo factor.
- Si los factores tienen diferente signo, el resultado tendrá signo negativo. Para obtenerlo, al igual que en el caso anterior, se debe sumar un factor a sí mismo el número de veces que indique el otro factor.
- Si el divisor y el dividendo tienen igual signo, el cociente tendrá signo positivo. Para obtener el resultado, se debe distribuir el dividendo en partes iguales entre el número que dice el divisor.
- Si el divisor y dividendo tienen signos distintos, el cociente tendrá signo negativo. El resultado se obtiene de la misma forma que en el ejemplo anterior.
Ejemplo:
a) 4 x 5 = 20
Donde, el primer factor, 4, se suma a sí mismo 5 veces. Dando como resultado 20. El signo del producto es positivo porque los signos de ambos factores son iguales.
b) -3 x -6 = 18
Donde, el número 6, uno de los factores, se suma a sí mismo 3 veces, el valor del otro factor, dando como resultado 18. El signo del producto es positivo (+) porque los signos de ambos factores son iguales, sin importar que sean negativos.
Ejemplo
a) 8 x -2 = -16
Donde, el factor 8 se suma a sí mismo 2 veces, que corresponde al segundo factor. Como los signos de ambos factores son distintos, el resultado o producto tendrá signo negativo (-).
Para la división, el resultado de la operación se denomina cociente, el número que se divide, se llama dividendo y el número por el cual se está dividiendo se denomina divisor.
Al igual que para la multiplicación, en la división se usa la misma regla de signos.
Ejemplo:
a) 25 : 5 = 5
Donde, el dividendo es 25 y debe distribuirse en partes iguales entre 5, el valor del divisor. Entonces el 25 (dividendo) se divide en 5 grupos (divisor) de 5 unidades cada uno (cociente). El resultado será positivo dado que los signos del divisor y dividendo son iguales.
b) -14 : -7 = 2
Donde, el 14 (dividendo) debe distribuirse en 7 grupos (divisor), dando como resultado 2 unidades por grupo (cociente). El signo del resultado es positivo (+) dado que los signos del divisor y dividendo son iguales.
Ejemplo:
-36 : 9 = -4
Donde, el valor del dividendo es 36, el cual se debe distribuir en partes iguales en 9 grupos (divisor), dando como resultado 4 unidades por grupo (cociente). El cociente es negativo dado que los signos del divisor y dividendo son distintos.
En la siguiente tabla se puede observar las reglas a seguir para la multiplicacióm y división de números enteros.
MULTIPLICACIÓN Y DIVISIÓN |
||
|---|---|---|
Ejemplos de números enteros

El primer ejemplo básico radica en cualquiera de los digitos enteros existentes es decir, 1, 2, 3, 4, 5, 6, 10, 590, 880, 930, 112. Claro está, también aplican los números negativos que le corresponden, es decir, -1, -2, -3, -4, -5, -6, -10, -590, -880, -930, -112.
En cuantos a los ejercicios con números enteros:
- 3 – (-4) = 3 + (4) = 3 + (4) = 7
- (-3) – (-4) = (-3) + (4) = 4 – 3 = 1
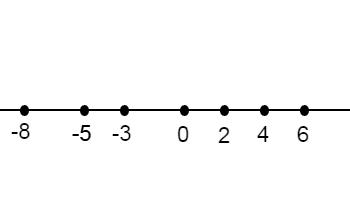
- Representar gráficamente los siguientes números enteros: -3, 0, 2, 4, -5, 2, 6, -8.
- Calcular el valor absoluto de:
- -4 = |-4| = 4
- -1 = |-1| = 1
- 0 = |0| = 0
- 34 = |34| = 34