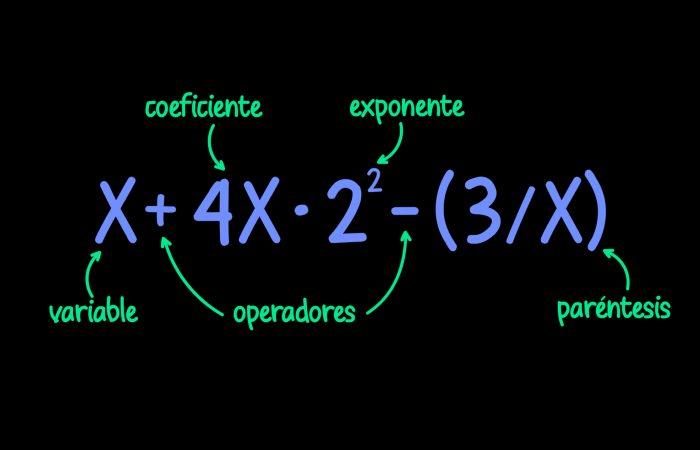Qué son las expresiones algebraicas
Como se mencionó con anterioridad, dichas operaciones no son más que la combinación de letras, números y signos que, posteriormente, se emplean en diferentes operaciones de tipo matemático. En las expresiones algebraicas, las letras tienen el comportamiento de los números y cuando estas toman ese curso, se emplean entre una y dos letras.
Sin importar la expresión que se tenga, lo primero que se debe hacer es simplificar, esto se logra utilizando las propiedades de la o las operaciones, mismas que son equivalentes a las propiedades numéricas. Para encontrar el valor numérico de una operación algebraica, se debe sustituir la letra por un número determinado.
Se pueden realizar muchos ejercicios sobre estas expresiones y se harán en este apartado para mejorar el entendimiento del tema en cuestión.
Expresiones algebraicas ejemplos:
- (X + 5/X + 2) + (4X + 5/X + 2)
X + 5 + 4X + 5/ X + 2
5X + 10/X + 2
5(X + 2)/X + 2
5 - (3/X + 1) – (1/X + 2)
3(X+2) – X – 1/(X + 1)*(X + 2)
2X – 5/X^2 + 3X + 2
Lenguaje algebraico
El lenguaje algebraico es aquel que emplea símbolos y letras para representar números. Su función principal es establecer y estructurar un lenguaje que ayude a generalizar las diferentes operaciones que tienen lugar dentro de la aritmética donde solo ocurren los números y sus operaciones aritméticas elementales (+ -x%).
El lenguaje algebraico tiene como finalidad, establecer y diseñar un idioma que ayude a generalizar las diferentes operaciones que se desarrollen dentro de la aritmética, donde sólo se emplean los números y sus operaciones matemáticas básicas: suma (+), resta (-), multiplicación (x) y división (/).
El idioma algebraico se caracteriza por su precisión, ya que es mucho más concreto que el lenguaje numérico. A través de él se pueden expresar enunciados de manera breve. Ejemplo: el conjunto de los múltiplos de 3 es (3, 6, 9, 12…) se expresa 3n, en donde n = (1, 2, 3, 4…).
Permite expresar números desconocidos y realizar operaciones matemáticas con ellos. Ejemplo, la suma de dos números se expresa así: a+b. Admite la expresión de relaciones y propiedades numéricas de carácter general.
Ejemplo: la propiedad conmutativa se expresa así: a x b = b x a. Al escribir utilizando este lenguaje se puede manipular cantidades desconocidas con símbolos sencillos de escribir, permitiendo la simplificación de teoremas, formulación de ecuaciones e inecuaciones y el estudio de cómo resolverlas.
Signos y símbolos algebraicos
En álgebra, se emplean tanto símbolos como signos en la teoría de conjuntos y estos constituyen o representan ecuaciones, series, matrices, etc. Las letras son expresadas o denominadas como variables, pues se usa la misma letra en otros problemas y, su valor encuentra diferentes variables. Entre algunas de las expresiones algebraicas clasificación se encuentran los siguientes:
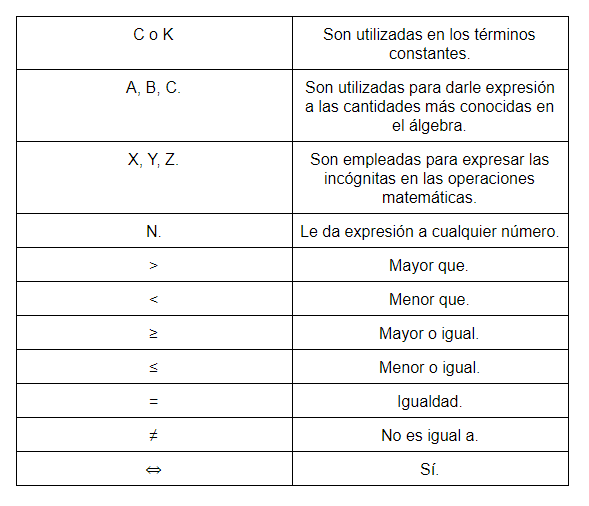
Fracciones algebraicas
Se conoce como una fracción algebraica aquella que está representada por el cociente de dos polinomios que muestran un comportamiento similar a las fracciones numéricas. En matemáticas, se puede operar con dichas fracciones realizando multiplicaciones y divisiones. Por lo tanto, se debe expresar que la fracción algebraica está representada por el cociente de dos expresiones algebraicas donde el numerador es el dividendo y el denominador el divisor.
Entre las propiedades de las fracciones algebraicas se puede resaltar que si el denominador se divide o multiplica por la misma cantidad diferente de cero, la fracción no se verá alterada. La simplificación de una fracción algebraica consiste en transformarla en una fracción que ya no se puede reducir, siendo necesario factorizar los polinomios que componen el numerador y el denominador.
Las expresiones algebraicas clasificación se reflejan en los siguientes tipos: equivalente, simple, correcto, impropio, compuesto de numerador o denominador nulo. Entonces veremos cada uno de ellos.
Equivalentes
Se está frente a esta vertiente cuando el producto cruzado es el mismo, es decir cuando el resultado de las fracciones es igual. Por ejemplo, de estas dos fracciones algebraicas: 2/5 y 4/10 serán equivalentes si 2*10 = 5*4.
Simples
Son aquellas en las que el numerador y el denominador representan expresiones racionales enteras.
Propias
Son fracciones simples en las que el numerador es menor que el denominador.
Impropias
Son fracciones simples en las cuales el numerador es igual o mayor que el denominador.
Compuestas
Son las formadas por una o más fracciones que se pueden ubicar en el numerador, el denominador o ambos.
De numerador o denominador nulo
Se presenta cuando el valor es 0. En el caso de tener una fracción 0/0 será indeterminado. Al usar las fracciones algebraicas para realizar operaciones matemáticas, se deben tener en cuenta algunas características de las operaciones con fracciones numéricas, por ejemplo, para iniciar se debe encontrar el mínimo común múltiplo cuando los denominadores son de dígitos diferentes.
Tanto en la división como en la multiplicación, las operaciones se realizan y se llevan a cabo igual que con las fracciones numéricas, ya que estas deben simplificarse previamente siempre y cuando le sea posible.
Monomios

Los monomios son expresiones algebraicas ampliamente utilizadas que cuentan con una constante que se llama coeficiente y una parte literal, que se representa con letras y se puede elevar a diferentes potencias. Por ejemplo, el monomial 2x² tiene 2 como su coeficiente y x² es la parte literal.
En varias ocasiones, la parte literal puede estar compuesta por una multiplicación de incógnitas, por ejemplo en el caso de 2xy. Cada una de estas letras se llama indeterminada o variables. Un monomio es un tipo de polinomio con un solo término, además, existe la posibilidad de estar frente a monomios semejantes.
Elementos de los monomios
Dado el monomio 5x^3 ; se distinguen los siguientes elementos:
- Coeficiente: 5
- Parte literal: x^3
El producto de monomios es el coeficiente, el cual se refiere al número que aparece multiplicando la parte literal. Por lo general, se coloca al principio. Si el producto de monomios tiene valor 1, no está escrito, y nunca puede ser cero, ya que la expresión completa tendría valor cero. Si hay algo que se debe saber de los monomios ejercicios, es que:
- Si un monomio carece de un coeficiente, es igual a uno.
- Si cualquier término no tiene exponente, es igual a uno.
- Si alguna parte literal no está presente, pero es necesaria, se considera con un exponente de cero.
- Si nada de esto concurre, entonces no se está frente a monomios ejercicios, incluso se podría decir que existe la misma regla con los ejercicios entre polinomios y monomios.
Suma y resta de monomios
Para poder realizar sumas entre dos monomios lineales, es necesario mantener la parte lineal y sumar los coeficientes. En las restas de dos monomios lineales, se debe mantener, al igual que en las sumas, la parte lineal para poder restar los coeficientes, luego se multiplican los coeficientes y se suman los exponentes con las mismas bases.
Multiplicación de monomios
Se trata de un monomio cuyo coeficiente es el producto o resultado de los coeficientes, las cuales tienen una parte literal que ha sido obtenida a través de la multiplicación de potencias que tienen exactamente la misma base.
División de monomios
No es más que otro monomio cuyo coeficiente es el cociente de los coeficientes obtenidos que, además, poseen una parte literal obtenida de las divisiones entre las potencias que tienen exactactamente la misma base.
Polinomios
Cuando hablamos de polinomios, se hace referencia a una operación algebraica de sumas, restas y multiplicaciones ordenadas hechas de variables, constantes y exponentes. En álgebra, un polinomio puede tener más de una variable (x, y, z), constantes (enteros o fracciones) y exponentes (que solo pueden ser números enteros positivos).
Los polinomios están formados por términos finitos, cada término es una expresión que contiene uno o más de los tres elementos con los que están hechos: variables, constantes o exponentes. Por ejemplo: 9, 9x, 9xy son todos términos. Otra forma de identificar los términos es que están separados por sumas y restas.
Para resolver, simplificar, sumar o restar polinomios, hay que juntar los términos con las mismas variables que, por ejemplo, los términos con x, los términos con “ y” y los términos que no tienen variables. Además, es importante observar el signo que está antes del término que determinará si agrega, resta o multiplica. Los términos con las mismas variables se agrupan, agregan o restan.
Tipos de polinomios
El número de términos que tiene un polinomio indicará qué tipo de polinomio es, por ejemplo, si hay un polinomio de un solo término, entonces se está frente a un monomio. Un claro ejemplo de esto es unos de los polinomios ejercicios (8xy). También está el polinomio de dos términos, el cual es denominado binomial y se identifica por el siguiente ejemplo: 8xy – 2y.
Por último, el polinomio de tres términos, los cuales se conocen como trinomios y se identifica por uno de los polinomios ejercicios de 8xy – 2y + 4. Los trinomios son un tipo de expresión algebraica formada por la suma o la diferencia de tres términos o monomios (monomios semejantes).
También es importante hablar del grado de polinomio, pues si este es de una sola variable es el mayor exponente. El grado de un polinomio con más de una variable se determina mediante el término con el mayor exponente.
Suma y resta de polinomios
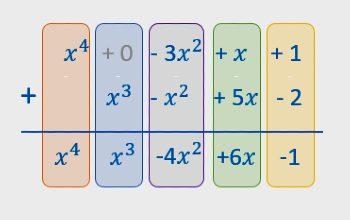
La suma de polinomios implica combinar términos. Los términos similares se refieren a los monomios que tienen la misma variable o variables elevadas a la misma potencia.
Existen diferentes maneras de realizar cálculos con polinomios, entre ellos, la suma de polinomios, la cual se puede hacer de dos maneras diferentes: horizontal y verticalmente.
- Suma de polinomios en horizontal: es empleada para hacer operaciones horizontalmente, valga la redundancia, pero primero se escribe un polinomio y luego se sigue en la misma línea. Posterior a ello, se escribe el otro polinomio que se va a sumar o restar y finalmente, se agrupan los términos similares.
- Suma de polinomios vertical: se logra escribiendo el primer polinomio de manera ordenada. Si este se encuentra incompleto, es importante dejar los huecos de los términos faltantes libres. Luego, se escribe el polinomio siguiente justo debajo del anterior, de esta manera, el término similar al de arriba va a quedar debajo. Finalmente se agrega cada columna.
Es importante agregar que para sumar dos polinomios, los coeficientes de los términos del mismo grado se deben sumar. El resultado de agregar dos términos del mismo grado, es otro término del mismo grado. Si falta algún término de cualquiera de los grados, se puede completar con 0. Y generalmente se ordenan de mayor a menor grado.
Como se mencionó anteriormente, para realizar la suma de dos polinomios, solo se necesita sumar los términos de mismo un grado. Las propiedades de esa operación se conforman por:
- Propiedades asociativas: en las cuales la suma de dos polinomios se resuelve agregando los coeficientes que acompañan a las x que se elevan a la misma potencia.
- Propiedad conmutativa: la cual altera el orden de la suma y no se logra deducir el resultado. Los elementos neutrales, los cuales tienen todos sus coeficientes igual a 0. Cuando se agrega un polinomio al elemento neutro, el resultado es igual al primero.
- Propiedad opuesta: formada por el polinomio que tiene todos los coeficientes inversos a los coeficientes del polinomio agregado. así, al realizar la operación de suma, el resultado es el polinomio nulo.
Con respecto a la resta de polinomios, (operaciones con polinomios) resulta imperativo hacer la agrupación de monomios de acuerdo a las características que poseen y comenzar con la simplificación de los que resultaron semejantes. Las operaciones con polinomios se realizan sumando el opuesto del sustraendo al minuendo.
Otra manera eficaz de proceder con la resta polinomios, es escribir el opuesto de cada polinomio debajo del otro. Así, los monomios semejantes quedan en columnas y se procede a sumarlos. No importa cuál técnica se lleve a cabo, al final, el resultado siempre será el mismo, claro, si se realiza correctamente.
Multiplicación de polinomios
Multiplicación de monomios o ejercicios entre polinomios y monomios, es una operación que se lleva a cabo para encontrar el producto resultante, entre un monomio (expresión algebraica basada en la multiplicación de un número y una carta elevada a un exponente entero y positivo) y otra expresión, si este es un término independiente, otro monomio o incluso un polinomio (suma finita de monomios y términos independientes).
Sin embargo, como ocurre con casi todas las operaciones matemáticas, la multiplicación de polinomios también tiene una serie de pasos que se deben seguir al resolver la operación propuesta, que se puede resumir en los siguientes procedimientos:
Lo primero que se debe hacer es multiplicar el monomio por su expresión (multiplicar los signos de cada uno de sus términos). Posterior a ello, se multipliquen los valores de coeficientes y al encontrar el valor en esa operación, se le agrega el literal de los monomios encontrados en los términos. Luego se anota cada resultado en orden alfabético y, finalmente, se agrega cada exponente, mismos que se ubican en los literales de la base.
División de polinomios

También conocido como el método de Ruffini. Nos permite dividir un polinomio entre un binomio y además permite localizar las raíces de un polinomio para factorizarlo en binomios. En otras palabras, esta técnica posibilita dividir o descomponer un polinomio algebraico de grado n, en un binomio algebraico, y luego en otro polinomio algebraico de grado n-1. Y para que esto sea posible se necesita saber o conocer por lo menos una de las raíces del polinomio único, con el propósito de que la separación sea exacta.
Es una técnica eficaz para dividir un polinomio por un binomio de la forma x – r. La regla de Ruffini es un caso especial de la división sintética cuando el divisor es un factor lineal. El método de Ruffini fue descrito por el matemático, profesor y médico italiano Paolo Ruffini en el año de 1804, quien además de inventar el famoso método denominado regla de Ruffini, que ayuda a encontrar los coeficientes del resultado de la fragmentación de un polinomio por el binomio; también descubrió y formuló esta técnica sobre el cálculo aproximado de las raíces de las ecuaciones.
Como siempre, cuando se trata de una operación algebraica, la Regla de Ruffini implica una serie de pasos que deben cumplirse para llegar al resultado deseado, en este caso: encontrar el cociente y el resto inherentes en la división de cualquier tipo de polinomio y un binomio de forma x + r.
En primer lugar, al momento de dar inicio con la operación, hay que revisar las expresiones para verificar o determinar si realmente se tratan como polinomios y binomios que responden a la forma esperada por el método de la Regla de Ruffini.
Una vez que se verifiquen estos pasos, se procede a ordenar el polinomio (en orden descendente). Finalizado este paso, se toma en cuenta únicamente a los coeficientes de los términos del polinomio (hasta el independiente) colocándolos en fila de izquierda a derecha. Se dejan algunos espacios para los términos que hagan falta (solo en caso de un polinomio incompleto). Se coloca el signo de galera en la izquierda de la fila, la cual está conformada por coeficientes del polinomio de dividendos.
En la parte izquierda de la galera, se procede a colocar el término independiente del binomio, que, ahora, es divisor y su signo es inverso. El independiente se multiplica por el primer coeficiente del polinomio, registrándose así en una segunda fila debajo del primero. Luego se resta el segundo coeficiente y el producto del término independiente monomial por el primer coeficiente.
El término independiente del binomio es multiplicado por el resultado de la resta anterior. Pero además, se coloca en la segunda fila, la cual le corresponde al cuarto coeficiente. La operación se repite hasta llegar a todos los términos. La tercera fila que se ha obtenido en base a estas multiplicaciones se toma como un cociente, con la excepción de su último término, que se considerará como el resto de la división.
El resultado se expresa, acompañando cada coeficiente de la variable y el grado que le corresponde, comenzando a expresarlos con un grado menor que el que tenían originalmente.
- Teorema del resto: es un método práctico que se usa para dividir un polinomio P (x) por otro cuya forma es xa; en el que solo se obtiene el valor del resto. Para aplicar esta regla, se siguen los siguientes pasos. Se escribe el dividendo polinomial sin completar u ordenar, luego se reemplaza la variable x del dividendo con el valor opuesto del término independiente del divisor. Y, finalmente, las operaciones se resuelven combinadas.
El teorema del resto es un método por el cual podemos obtener el residuo de una división algebraica pero en la cual no es necesario hacer ninguna división.
Esto nos permite averiguar el resto de la división de un polinomio p (x) entre otro de la forma x-a, por ejemplo. De este teorema se desprende que un polinomio p (x) es divisible por x-a solo si a es una raíz del polinomio, solo si y sólo si p (a) = 0. Si C (x) es el cociente y R (x) es el resto de la división de cualquier polinomio p (x) entre un binomio que sería (x-a) el valor numérico de p (x), para x = a, es igual al resto de su división entre x-a.
Entonces diremos que: nP (a) = C (a) • (a – a) + R (a) = R (a). En general, para obtener el resto de una división entre X-a, es más conveniente aplicar la regla de Ruffini que reemplazar la x. Por lo tanto, el teorema del resto es el método más adecuado para resolver problemas.
-
Método de Ruffini: el método o regla de Ruffini es un método que nos permite dividir un polinomio entre un binomio y además permite localizar las raíces de un polinomio para factorizar en binomios. En otras palabras esta técnica posibilita dividir o descomponer un polinomio algebraico de grado n, en un binomio algebraico, y luego en otro polinomio algebraico de grado n-1. Y para que esto sea posible se necesita saber o conocer por lo menos una de las raíces del polinomio único, con el propósito de que la separación sea exacta.
En el mundo matemático, a regla de Ruffini es una técnica eficaz para dividir un polinomio por un binomio de la forma x – r. La regla de Ruffini es un caso especial de la división sintética cuando el divisor es un factor lineal.
El método de Ruffini fue descrito por el matemático, profesor y médico italiano Paolo Ruffini en el año de 1804, quien además de inventar el famoso método denominado regla de Ruffini, que ayuda a encontrar los coeficientes del resultado de la fragmentación de un polinomio por el binomio; también descubrió y formuló esta técnica sobre el cálculo aproximado de las raíces de las ecuaciones.
- Raíces de polinomios: las raíces de un polinomio son ciertos números que hacen que un polinomio valga cero. También podemos decir que las raíces completas de un polinomio de coeficientes enteros serán divisores del término independiente. Cuando resolvemos un polinomio igual a cero, obtenemos las raíces del polinomio como soluciones. Como propiedades de las raíces y los factores de los polinomios podemos decir que los ceros o raíces de un polinomio están por los divisores del término independiente que pertenece al polinomio.
Luego, para cada raíz, por ejemplo, del tipo x = a corresponde a un binomio del tipo (x-a). Es posible expresar un polinomio en factores si lo expresamos como un producto de todos los binomios del tipo (x-a) que corresponden a las raíces, x = a, que resultan. Se debe tener en cuenta que la suma de los exponentes de los binomios es igual al grado del polinomio, también se debe tomar en cuenta que cualquier polinomio que no tenga un término independiente admitirá como raíz x = 0, en otra forma, admitirá como un factor x.
Llamaremos a un polinomio «primo» o «Irreducible» cuando no hay posibilidad de descomponerlo en factores.
Para profundizar en el tema debemos tener claro el teorema fundamental del álgebra, que expresa que basta que un polinomio en una variable no constante y coeficientes complejos, posee tantas raíces como su grado, ya que las raíces tienen sus multiplicidades. Se confirma con esto que cualquier ecuación algebraica de grado n posee n soluciones complejas. Un polinomio de grado n tiene un máximo de n raíces reales.
Ejemplos y ejercicios
En este apartado se colocarán algunas expresiones algebraicas ejercicios resueltos de cada uno de los temas abarcados en este post.
Expresiones algebraicas ejercicios:
- X^2 – 9/2X + 6
(X + 3) * (X – 3)/2 * (X + 3)
X – 3/2 - X^2 + 2X + 1/X^2 – 1
(X + 1)^2/(X + 1) * (X – 1)
X + 1/X – 1
Suma de polinomios
- 2x+3x+5x= (2+3+5) x= 10 x
- P(x)= 2×2+5x-6
Q(x)= 3×2-6x+3
P(x)+Q(x)= (2×2+5x-6)+ (3×2-6x+3)= (2×2+3×2) + (5x-6x) + (-6+3) = 5×2-x-3
Resta de polinomios
P(x)= 2×2+5x-6
Q(x)= 3×2-6x+3
P(x)-Q(x)= (2×2+5x-6)-(3×2-6x+3)= (2×2+5x-6) + (-3×2+6x-3)=(2×2-3×2) + (5x+6x) + (-6-3)= -x2+11x-9
División de polinomios
- 8 a / 2 a = (8/2).(a/a)= 4
- 15 ay /3a = (15/3) (a.y)/ a = 5 y
- 12 bxy / -2 bxy = (12/-2) (b.x.y)/(bxy.) = -6
- -6 v2.c. x/-3vc= (-6/-3) (v2.c. x) /(v. c) = 2 v
Expresiones algebraicas (binomio al cuadrado)
(x + 3)2 = x 2 + 2 • x •3 + 32 = x 2 + 6 x + 9
(2x − 3)2 = (2x)2 − 2 • 2x • 3 + 32 = 4×2 − 12 x + 9
Teorema de resto
(x4 − 3×2 + 2):(x − 3)
R=P(3) = 34 − 3 • 32 + 2 = 81 − 27 + 2 = 56
Multiplicación de monomios
axn · bxm = (a · b)xn + m
(5x²y³z) · (2y²z²) = (2 · 5) x²y3+2z1+2 = 10x²y5z³
4x · (3x²y) = 12x³y
División de monomios
8 a / 2 a = (8/2).(a/a)= 4
15 ay /3a = (15/3) (a.y)/ a = 5 y
12 bxy / -2 bxy = (12/-2) (b.x.y)/(bxy.) = -6
-6 v2 . c. x/-3vc= (-6/-3) (v2 .c. x) /(v. c) = 2 v
Suma y resta de monomios
Ejercicio: 3×3 – 4x + 5 – 2 + 2×3 + 2×2
Solución: 3×3 – 4x + 5 – 2 + 2×3 + 2×2 = 3×3 + 2×3 + 2×2 – 4x + 5 -2 = 5×3 + 2×2 – 4x + 3