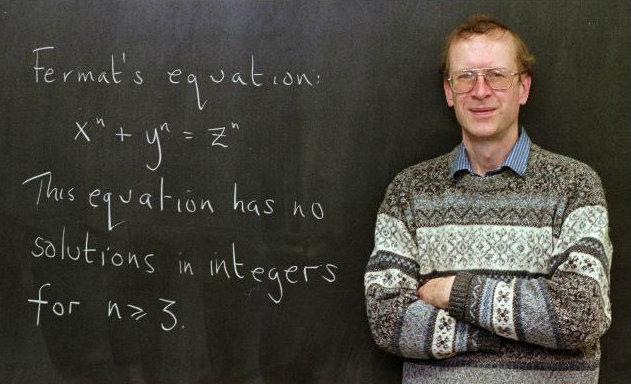Finalmente, pudo ser resuelto por Andrew Wiles en el año 1995, Wiles con la colaboración del matemático Richard Taylor, lograron la hazaña de poder demostrar este teorema, basándose en el Teorema de Taniyama Shimura. Si este teorema el cual afirma que si toda ecuación elíptica tiene que ser modular, era incorrecta, entonces también era falso el teorema de Fermat. Alcanzando la respuesta del último teorema de Fermat.
Wiles, reunió todas las ideas del problema que lo había seducido desde la infancia, busco la forma de evidenciar la existencia de una curva elíptica asociada a cada forma modular, al hacer esto, se encontraba con el teorema de Taniyama Shimura, el cual aplicó al de Fermat, y aunque encontró un error en su primera demostración, este fue resuelto. Wiles logró resolver uno de los problemas más complicados de la historia transformándose en uno de los más célebres matemáticos aún vivos. Siendo galardonado con el premio Abel apreciado por todos como el nobel de las matemáticas. Y el cual es otorgado por la Academia Noruega de Ciencias y Letras que anualmente otorga este famoso galardón de las matemáticas.