Qué es una ecuación
Es una igualdad matemática existente entre dos expresiones, estas son conocidas como miembros pero que están separadas por un signo (=), en estas, existen elementos conocidos y algunos datos o incógnitas que se relacionan a través de operaciones matemáticas. Los valores son números, constantes o coeficientes, aunque también pueden ser objetos como vectores o variables.
Los elementos o incógnitas se establecen a través de otras ecuaciones, pero con un procedimiento de resolución de ecuaciones. Un sistema de ecuaciones de estudia y resuelve mediante diferentes métodos, de hecho, ocurre lo mismo con la ecuación de la circunferencia.
El término nace del latín «aequatio», cuyo significado hace alusión a igualar.
Historia de las ecuaciones
La civilización egipcia fue una de las primeras en utilizar datos matemáticos, pues para el siglo XVI ya aplicaban dicho sistema, para resolver problemas asociados con la repartición de alimentos, aunque no eran llamados ecuaciones, se podría decir que es el equivalente a la época actual.
Durante la edad media, las incógnitas matemáticas tuvieron un gran impulso, pues estas eran utilizadas como desafíos públicos entre los matemáticos expertos de la época. Para el siglo XVI dos importantes matemáticos realizaron el descubrimiento de utilizar números imaginarios para poder solucionar los datos de segundo, tercer y cuarto grado.
También en ese siglo Rene Descartes hizo famosa la notación científica, además de ello, en esta etapa histórica se hizo público también uno de los teoremas más populares de la matemáticas “el último teorema de Fermat”.
Durante el siglo XVII los científicos Gottfried Leibniz e Isaac Newton hicieron posible la solución de las incógnitas diferenciales, lo que dio origen a una serie de descubrimientos que se dieron durante esa época con respecto a esas ecuaciones en específico.
Muchos fueron los esfuerzos que hasta principios del siglo XIX realizaron los matemáticos para encontrar la solución a las ecuaciones de quinto grado, pero todos fueron intentos fallidos, hasta que Niels Henrik Abel descubrió que no existe un fórmula general para calcular las de quinto grado, también durante esta época la física utilizó datos diferenciales en incógnitas integrales y derivadas, lo que dio origen a la física matemática.
En el siglo XX se formularon las primeras ecuaciones diferenciales con funciones complejas utilizadas en la mecánica cuántica, las cuales tienen un amplio campo de estudio en teoría económica.
También se debe hacer alusión a la ecuación de Dirac, la cual forma parte de los estudios de las ondas relativistas de mecánica cuántica y que fue formulada en 1928 por Paul Dirac. La ecuación de Dirac en totalmente consistente con la teoría de la relatividad especial.
Características de las ecuaciones
Estos ejercicios también poseen una serie de características o elementos específicos, entre ellos, los miembros, términos, incógnitas y soluciones. Los miembros son aquellas expresiones que se encuentran justo a los lados de los signos de igualdad. Los términos son aquellos sumandos que forman parte de los miembros, asimismo, las incógnitas hace alusión a las letras y por último, las soluciones, las cuales hacen referencia a los valores que verifican la igualdad.
Tipos de ecuaciones

Existen diferentes tipos de ejercicios matemáticos que han sido enseñados en los diferentes niveles de educación, por ejemplo, la ecuación de la recta, ecuación química, balanceo de ecuaciones o los diferentes sistema de ecuaciones, sin embargo, es importante mencionar que estas se clasifican en datos algebraicos, las cuales a su vez pueden ser de primero, segundo y tercer grado, diofánticas y racionales.
Ecuaciones algebraicas
Se trata de una valoración que se expresa en forma de P(x) = 0 en la cual P(x) es un polinomio que no es nulo pero tampoco constante y que posee coeficientes enteros con un grado n ≥ 2.
- Lineales: es una igualdad que posee una o más variables en la primera potencia y no necesita de productos entre dichas variables.
- Cuadráticas: posee una expresión de ax² + bx +c = 0 teniendo a ≠ 0. aquí la variable es x, y a, b y c son constantes, el coeficiente cuadrático es a, el cual es distinto de 0. El coeficiente lineal es b y el término independiente es c.
Se caracteriza por ser un polinomio que se interpreta a través de la ecuación de la parábola.
- Cúbicas: los datos cúbicas que poseen una incógnita se reflejan en tercer grado con a, b, c y d (a ≠ 0), cuyos números forman parte de un cuerpo de números reales o complejos, sin embargo, también hacen referencia a dígitos racionales.
- Bicuadráticas: es una expresión algebraica de una sola variable, de cuarto grado, que tiene solo tres términos: uno de grado 4, uno de grado 2 y un término independiente. Un ejemplo de un ejercicio biquad es la siguiente: 3x^4 – 5x^2 + 1 = 0 .
Recibe este nombre porque intenta expresar cuál será el concepto clave para delinear una estrategia de resolución: bi-cuadrado significa: «dos veces cuadrático». Si lo piensas, el término x4 puede expresarse como (x 2) elevado a 2, lo que nos da x4. En otras palabras, hay que imaginar que el término principal de la incógnita es 3×4. De igual manera es correcto decir que este término también se puede escribir como 3 (x2) 2.
- Diofantinas: es un ejercicio algebraico que posee dos o más incógnitas, además, sus coeficientes engloban todos los números enteros de los cuales se deben buscar las soluciones naturales o enteras. Esto hace que formen parte del grupo numérico entero.
Estos ejercicios se presentan como a x + b y = c con la propiedad de una condición suficiente y necesaria para que a x + b y = c con a , b , c que pertenece a los números enteros, tenga solución.
- Racionales: se definen como el cociente de los polinomios, mismos en los que el denominador tiene al menos 1 grado. Hablando de forma específica, debe existir aunque sea una variable en el denominador. La forma general que representa una función racional es:
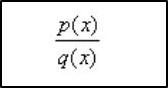
En la cual p ( x ) y q ( x ) son polinomios y q ( x ) ≠ 0.
- Equivalentes: es un ejercicio con igualdad matemática entre dos expresiones matemáticas, llamadas miembros, en la que aparecen elementos conocidos o datos, y desconocidos o incógnitos, relacionados por operaciones matemáticas. Los valoresde la ecuación deben estar formados por números, coeficientes o constantes; al igual que variables u objetos complejos como vectores o funciones, los elementos nuevos deben constituirse mediante otras ecuaciones de un sistema o algún otro procedimiento de resolución de funciones.
Ecuaciones trascendentes
No es más que una igualdad entre dos expresiones matemáticas que poseen una o más incógnitas que se relacionan a través de las operaciones matemáticas, mismas que son exclusivamente algebraicas y que tienen una solución que no puede darse utilizando las herramientas específicas o propias del álgebra. Una ejercicio H(x) = j(x) es denominado trascendente cuando una de las funciones H(x) o j(x) no es algebraica.
Ecuaciones diferenciales
En ellas se relacionan las funciones con cada una de sus derivadas. Las funciones tienden a representar ciertas cantidades físicas, por otro lado, las derivadas representan razones de cambio, mientras que la ecuación define la relación que existen entre ellas. Estas últimas tienen una importancia muy grande en muchas otras disciplinas, entre ellas, la química, biología, física, ingeniería y economía.
Ecuaciones integrales
La incógnita en las funciones de estos datos aparecen directamente en la parte integral. Los ejercicios integrales y diferenciales tienen muchísima relación, incluso algunos problemas matemáticos se puede formular con cualquiera de estas dos, un ejemplo de esto es el modelo de la viscoelasticidad de Maxwell.
Ecuaciones funcionales
Se expresa mediante la combinación de funciones incógnitas y de variables independientes, además, tanto su valor como su expresión se tiene que resolver.
Ecuaciones de estado
Se trata de ejercicios constitutivos para los sistemas hidrostáticos que describen el estado general de agregación o incremento de la materia, además, representa una relación entre el volumen, temperatura, densidad, presión, funciones de estado y la energía interna que se asocia con la materia.
Ecuaciones de movimiento
Es aquella enunciación matemática que explica el desarrollo temporal de una variable o grupo de variables que determinan el estado físico del sistema, con otras dimensiones físicas que promueven el cambio del sistema. Esta ecuación dentro de la dinámica del punto material, define la posición futura de un objeto en función de otras variables, como su masa, velocidad o cualquier otra que pueda afectar su movimiento.
El primer ejemplo de ecuación de movimiento dentro de la física fue mediante la segunda ley de newton para sistemas físicos compuestos de partículas y materiales puntuales.
Ecuaciones constitutivas
No es más que una relación entre las variables mecánicas o termodinámicas existentes en un sistema físico, es decir, donde exista tensión, presión, deformación, volumen, temperatura, entropía, densidad, etc. Todas las sustancias tienen una relación matemáticas constitutiva muy específica, la cual se basa en la organización molecular interna.
Resolución de ecuaciones

Para resolver las ecuaciones es completamente necesario encontrar su dominio solución, es decir, el conjunto o grupo de valores de incógnitas en los que se cumple su igualdad. Se puede emplear el uso de una calculadora de ecuaciones porque generalmente, estos problemas se expresan en uno o múltiples ejercicios.
También es importante mencionar que no todos estos ejercicios tienen solución, pues es bastante probable que no haya ningún valor en la incógnita que verifique la igualdad que se ha obtenido. En este tipo de casos, las soluciones de los ejercicios son vacíos y se expresa como ecuación irresoluble.
Ejemplos de ecuaciones
- De movimiento: ¿a qué velocidad debe transitar un automóvil de carreras para recorrer 50km en un cuarto de hora?. Debido a que la distancia se está expresando en kilómetros, se debe escribir el tiempo en las unidades de hora para tener la velocidad en km/h. Teniendo eso claro, entonces el tiempo que dura el movimiento es de:
- De estado: una masa de hidrógeno gaseoso está ocupando un volumen de 230 litros en un tanque, mismo en cual tiene la presión de 1.5 atmósfera y posee una temperatura de 35°C. Se debe calcular cuantos moles de hidrógeno se tienen y a cuanta masa equivale el número de moles contenidos en dicho tanque. Tomando todo eso cuenta, los datos son los siguientes:
- Constitutivas: hay 3 barras unidas a viga rígida. Los datos son: P= 15000 lbf, a = 5pie, b = 5pie, c = 8pie (1 pie=12 pulgadas).
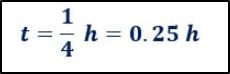
La distancia que recorre el auto es de:

Esto quiere decir que su velocidad debe ser ser:

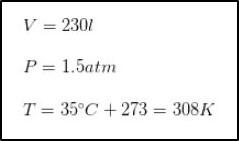
La fórmula es:
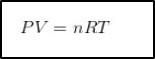
Por lo tanto, se debe dejar la “n”, y se obtiene:

Luego se sustituyen los datos:
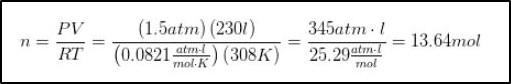
Y la cantidad de número de moles es de 13.64 moles.
Ahora se debe calcular la masa. Al tratarse de hidrógeno gaseoso, hay que hacer referencia a su peso atómico o masa molar, la cual es una molécula diatómica, compuesta por dos átomos de hidrógeno.
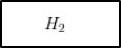
Su peso molecular es de 2 g/mol (debido a su característica diatómica), entonces se obtiene:

Es decir, que se ha obtenido una masa de 27.28 gramos.
La solución es que se asume que existen pequeñas deformaciones y que el tornillo es totalmente rígido, es por ello que al aplicar la fuerza P la viga AB rotaria rígidamente conforme al punto B.