Supongamos que tenemos un triángulo rectángulo ABC, con un ángulo de 90º y dos ángulos de 45º. Dividiendo una de las patas opuestas en un ángulo de 45º y la hipotenusa, obtendremos el seno y luego podemos calcular el coseno.
La trigonometría se aplicará donde sea necesario para obtener medidas precisas de algo, se aplica en la mayoría de las ramas de las matemáticas y también en otras disciplinas, tal es el caso de la astronomía para medir las estrellas más cercanas, las distancias de los puntos geográficos, y en el sistemas de navegación que involucran satélites. La geometría del espacio también hace uso de la trigonometría.
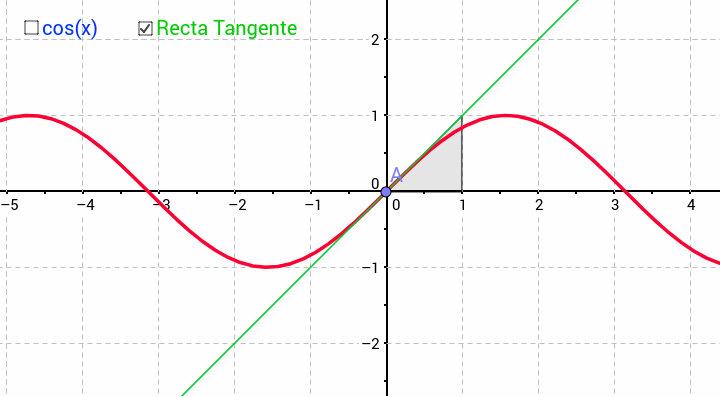
La trigonométrica es la función del coseno, el cual es el resultado del cociente entre la pierna adyacente y la hipotenusa. Dicho en fórmula:
Visto así, parece muy abstracto. Intenta pensar en una circunferencia, de radio uno. Luego, está la llamada circunferencia trigonométrica, que, al dividirla en cuadrantes, nos permite representar las relaciones trigonométricas de cualquier ángulo.
Una forma de obtener el coseno de un ángulo es representarlo en la circunferencia goniométrica, es decir, la circunferencia de la unidad centrada en el origen. En este caso, el valor del coseno coincide con la abscisa del punto de intersección del ángulo con la circunferencia. Esta construcción es lo que permite obtener el valor del coseno para ángulos no agudos.