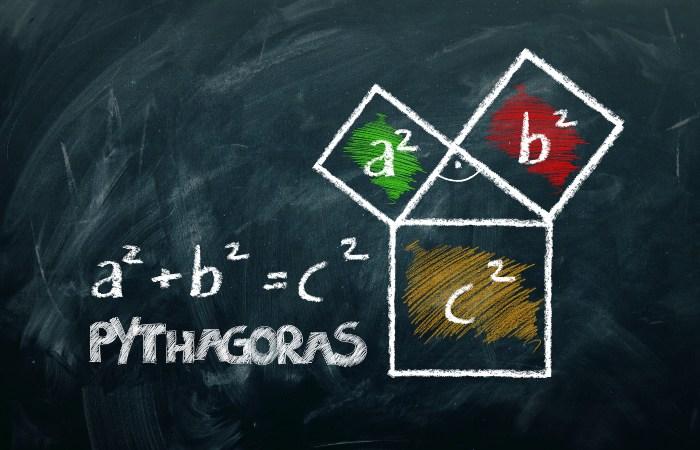Qué es teorema
Un teorema es una proposición en la cual se anuncia una verdad demostrable a través de leyes expresadas en ecuaciones, con argumentos dentro de un sistema formal, o con fórmulas matemáticas.
Un sinónimo de Teorema es el asumir la veracidad de un enunciado. Comprendiendo con esto que todo aquello llamado Teorema, en el campo matemático o filosófico, estaría sujeto a haber pasado por una comprobación previa de sus partes (Hipótesis, tesis y demostración), ejemplo, el teorema de Pitágoras, puede ser denominado Teorema porque todas las partes que lo comprenden han sido comprobadas, un ejemplo contrario sería la teoría de cuerdas, cuya teoría aún no puede ser verificada.
La palabra teorema proviene del griego θεώρημα (theórema), empleada alrededor del siglo 6.o A.C, por Thales de Mileto en sus trabajos geométricos, significa, examinar, observar, juzgar, analizar.
Características de un teorema
A continuación se mencionan las características de los teoremas:
- Un teorema reclama como requisito principal, partir de otro teorema, de una tesis, de un conjunto de axiomas, o de una hipótesis bien formulada.
- Es común que las herramientas para demostrar los elementos de un teorema, puedan ser similares a las que se emplean para demostrar otras técnicas, como el lema (perteneciente a un teorema teórico más largo), el corolario (que es lo que sigue al teorema), o la proposición (No se relaciona directamente a ningún teorema).
Partes de los teoremas
Indistintamente de la temática que tenga el teorema, debe poseer una estructura fija, que consta de tres partes.
Hipótesis
Es la suposición a comprobar, puede partir tanto de una tesis, un axioma, u otro teorema.
Tesis
Es aquello que debe ser demostrado una vez determinado el punto de partida y la estructura de la comprobación.
Demostración
Deberá ser el comprobante irrefutable que apoyara la tesis y afirmara que dicho teorema matemático o filosófico es cierto.
- La función de un teorema es tomar alguna información dada y brindarle un marco en la cual esta pueda ser expuesta, dando a conocer que es una fórmula o hipótesis bien formada y para la que existe una demostración irrefutable.
Tipos de teoremas
Existen muchos teoremas en la actualidad, consisten básicamente en comprobar hipótesis, por ejemplo los mencionados a continuación.
Teorema directo
También conocido como teorema recíproco, habla de cuando la hipótesis de un teorema matemático se relaciona directamente con la tesis de otro. Por ejemplo, el teorema directo señala que, si un número termina en cero o cinco (hipótesis), será divisible por cinco (tesis).
Teorema contrario
O también llamado teorema contra recíproco, habla de cuando la tesis de un teorema matemático se relaciona directamente con la hipótesis de otro. Por ejemplo: el teorema contrario señala que, si un número es divisible por cinco (hipótesis), tiene que terminar en cero o cinco (tesis).
Ejemplos de teoremas
De los muchos teoremas conocidos, algunos han sido un tanto mas conocidos gracias a sus aplicaciones prácticas, por ejemplo:
Teoremas de Fermat
No hay números positivos y enteros A, B y C que cumplan la igualdad An + Bn = Cn, si n es mayor o igual a tres. La fórmula que define este teorema es sin duda una de las más conocidas por su amplia aplicación en físicas y matemáticas, en distintas literaturas de estudio se dispone de una gran cantidad de ejercicios para este teorema.
Teorema de Moivre
Al tener un número complejo en forma polar, A = BƟ, en la que B es el módulo del número complejo A, y el ángulo Ɵ es llamado amplitud o argumento de cualquier número complejo con 0 ≤ Ɵ ≤ 2π, para calcular potencia n, no es necesario multiplicar por sí mismo n veces. Puede hacerse como a continuación, (cos x + i sin x) n = cos (nx) + i sin (nx).
Teorema de Thevenin
Establece que un circuito eléctrico, conectado en línea entre el terminal A y B, se podría sustituir dicha parte por un circuito equivalente, constituido por un generador de tensión en serie con una resistencia.
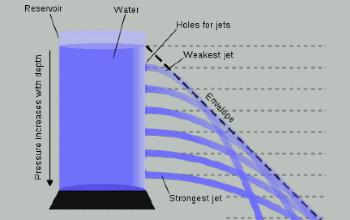
Teorema de Torricelli
Propuesto por Bernoulli, dice que a través de los principios de la mecánica de fluidos, el teorema comprueba la conducta de un fluido en movimiento, en el interior de un sistema cerrado. Este teorema se enfoca en la conducta que tiene un fluido al salir por la apertura de un recipiente cerrado. Su fórmula es
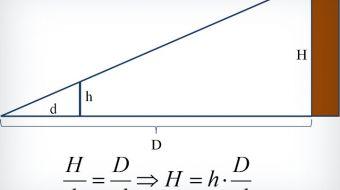
Teorema de Tales de Mileto
El cual lleva el nombre del matemático a quien se le atribuye, indica que una recta ubicada paralelamente a uno de los lados de un triángulo, formará junto a las otras dos extensiones, otro triángulo afín al triángulo principal.
Teorema de Pitágoras
El teorema lleva el nombre del filósofo griego, porque se atribuye la primera demostración de este teorema a la Escuela Pitagórica, y no a Pitágoras como tal. La teoría de este teorema consiste en que el cuadrado de la longitud de la hipotenusa de un triángulo rectángulo será igual a la suma de los cuadrados de las respectivas longitudes de los catetos. Ejemplo: