Las obras originales de Tales no se conservan, pero a través de otros pensadores e historiadores se conocen sus principales contribuciones: predijo el eclipse solar del año 585 a. C, defendió la idea de que el agua es el elemento original de la naturaleza y también se destacó como un matemático, siendo su contribución más reconocida el teorema que lleva su nombre. Según la leyenda, la inspiración para el teorema proviene de la visita de Thales a Egipto y la imagen de las pirámides.
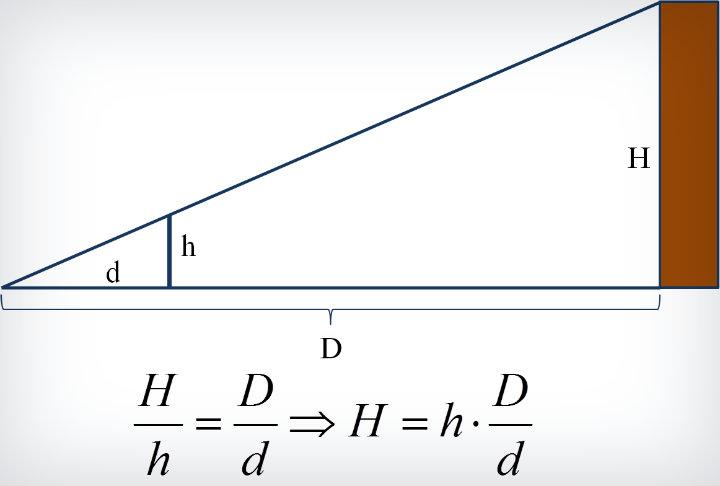
El enfoque geométrico del teorema de Thales tiene implicaciones prácticas obvias. Veamos con un ejemplo concreto: un edificio de 15 m de altura proyecta una sombra de 32 metros y, en el mismo momento, un individuo proyecta una sombra de 2.10 metros. Con estos datos es posible conocer la altura de dicho individuo, ya que es necesario tener en cuenta que los ángulos que proyectan sus sombras son congruentes. Por lo tanto, con los datos del problema y el principio del teorema de Thales en los ángulos correspondientes, es posible conocer la altura del individuo con una regla simple de tres (el resultado sería 0.98 m).
Otro teorema muy popular es el de Pitágoras, que indica que el cuadrado de la hipotenusa (es decir, el lado de mayor longitud y que se opone al ángulo recto), en un triángulo rectángulo, es idéntico a la suma de los cuadrados de las patas (es decir, el par de lados más pequeños del triángulo rectángulo). Sus aplicaciones son innumerables, tanto en el campo de las matemáticas como en la vida cotidiana.
De hecho, es uno de los teoremas más fáciles de usar y puede resolver muchos problemas sin conocimientos técnicos o avanzados. Hacer mediciones en superficies rectas, como pisos o paredes, es mucho más simple que extender un metro de un punto a otro dibujando una línea oblicua en el aire, especialmente si la distancia es tal que requiere varios pasos.