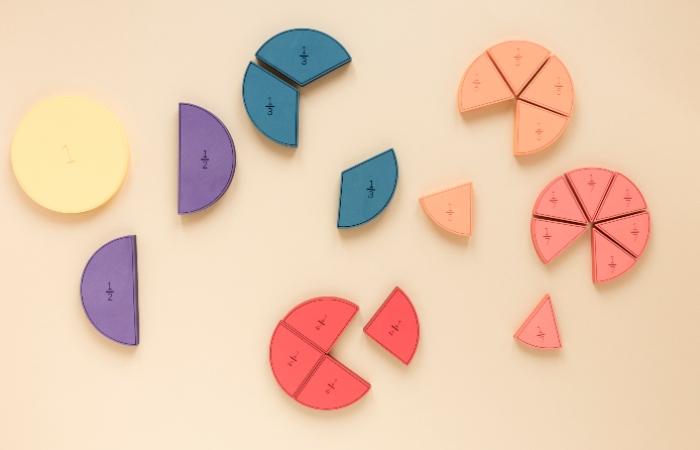Qué es una fracción
Una fracción es una expresión que se refiere a una división. Se compone de dos números separados por una línea divisoria: el numerador es el número que se divide, mientras que el denominador es la cantidad por la que se divide. Cuando el numerador y el denominador son iguales, sabemos que es entonces un número entero escrito en forma de una fracción, por ejemplo 6/6. Comúnmente se dice que este tipo de fracción es propia.
Las operaciones con fracciones son definidas como un grupo matemático plasmadas con la forma de A/B, en la cual tanto A como B son dígitos enteros y B≠0 no es más que el grupo de números racionales, los cuales se plasman con el símbolo ℚ.
Es importante destacar que todos los ejercicios de fracciones son divisiones, es por ello que se dice que las divisiones se convierten en una fracción únicamente para ser simplificadas, además, estas pueden representarse como A+B o A/B en las operaciones con fracciones.
De una forma más genérica, este término no es más que un cociente de expresiones matemáticas, esto quiere decir que no solo abarca dígitos, sino también símbolos. Debido a la evolución tecnológica y la necesidad de resolver estas operaciones, existe una calculadora de fracciones que facilita la solución del fraccionamiento matemático.
Este vocablo tiene su origen en el latín, específicamente la palabra “fractio”, el concepto de fracción se emplea para hacer referencia a un proceso basado en dividir algo en partes.
Características de las fracciones
De las características relevantes se pueden mencionar:
- El fraccionamiento matemático es una representación de repartos en partes iguales.
- Abarca términos como numerador y denominador
- El denominador es el encargado de indicar cuál es el número de trozos iguales en los cuales se puede dividir una unidad.
- No solo se trata de las suma y resta de fracciones, sino de la suma de fracciones con diferente denominador y la resta de fracciones con diferente denominador.
En la vida cotidiana también se hace uso de estas operaciones, sobre todo cuando se dice “vamos a mitad y mitad” al momento de hacer una compra o decir que “falta un cuarto de hora” para llegar a una cita.
Partes de una fracción
Una fracción se encuentra compuesta por dos términos: en primer lugar se tiene al numerador y seguidamente está el denominador. Por su parte el numerador es aquel número que se ubica sobre la raya fraccionaria y el denominador es el que está bajo la misma.
Representación gráfica de fracciones
Por lo general, para representar estas operaciones se hace uso de una figura geométrica que hace alusión a la unidad, esta se selecciona en una cantidad de trozos iguales, de modo que se pueda plasmar el denominador y se omiten las que destinadas a la distinción de la cantidad del numerador.
En operaciones comunes, el denominador es expresado como un dígito partitivo, es decir, ¼ es un cuarto. Las operaciones negativas son aquellas que tienen valor negativo y, además, las operaciones genéricas A/B son representadas con el producto de A por el multiplicativo de B.
Cuando A y B son dígitos negativos, entonces el producto es positivo. Es importante destacar que las expresiones genéricas de AB hacen alusión a divisiones algebraicas, esto quiere decir que el divisor tiene que ser distinto al cero, pues el cociente de la operación contienen un número decimal en el sistema de numeración decimal que tiende a ser finito o infinito periódico. Los dígitos racionales no abarcan escrituras en números de tipo fraccionario, pues su expansión decimal es infinita y no periódica, por ejemplo, el número pí, el E y el áureo en conjunto con raíces cúbicas y cuadradas.
Tipos de fracciones
Tal como sucede con cualquier operación matemática, esta se divide en una serie de tipos o vertientes especiales, las cuales se clasifican de la siguiente forma.
Fracciones simples
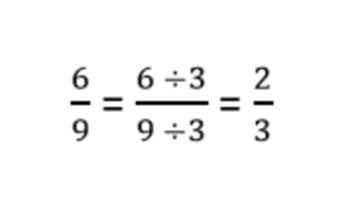
Son aquellas en las cuales el numerador y el denominador son primos, es decir, no tiene más factores comunes que el dígito 1. Ejemplo:
Entonces su forma simple es 2/3
Fracciones impropias
Son aquellas en las que el numerador es mayor que el denominador. Teniendo en cuenta esta explicación, se puede afirmar que 4/3, para nombrar un caso, es una fracción impropia. Su numerador es 4 y su denominador, 3: como puede ver, el numerador es mayor que el denominador. Si resolvemos la división, notaremos que el resultado es mayor que 1: 1.33.
Fracciones propias
Se caracterizan porque el denominador es mayor respecto al numerador y no sobrepasan la unidad. Ejemplo, 20/73 y 64/133.
Fracciones mixtas
Tienen una característica particular, y es que delante del numerador y el denominador se escribe un número entero, por lo general dicho número es de mayor tamaño (en lo que se refiere a su tipografía) y ubicado en el centro vertical. Dicho valor indica qué cantidad de veces se completa el denominador, hecho que no sucede en el resto de las fracciones. Un ejemplo sería 4 1/3, lo que significa que se tienen 4 unidades (cuatro veces tres tercios) y un tercio.
Fracciones equivalentes
Sucede cuando el denominador y el numerador son multiplicados por el mismo dígito, ejemplo, 34 x 22 = 68, donde el ¾ es equivalente al fraccionamiento de 6/8.
Fracciones decimales
Se trata de aquellas operaciones en las cuales el denominador es una potencia de 10 (abarcando el 100, 1000, entre otros), por ejemplo, 43/100.
Resolución de fracciones
Se trata de la manera en la que se pueden resolver este tipo de operaciones aplicando sumas, restas, multiplicaciones y divisiones.
Multiplicación de fracciones
Para saber cómo multiplicar fracciones, es necesario entender que cualquier numerador tiene la capacidad de simplificar los denominadores, además, se multiplican los denominadores para la obtención del denominador dinal, de manera que se puedan multiplicar los numeradores y adquirir el numerador final de la operación. Ejemplo, 4/2 X 1/4 = 4X1/2X4 = 4/8
Resta de fracciones
Este tipo de operaciones se pueden realizar sin ejecutar otros pasos intermedios, pero solo cuando poseen el mismo denominador, solo se tiene que escribir el mismo denominador en la fracción que se obtiene como resultado, restar los numeradores y escribir los resultados.
Cuando se trata de diferentes denominadores se multiplica el numerador de la primera operación con el denominador de la segunda y el denominador de la primera con el numerador de la segunda. Las dos multiplicaciones se restan, luego se multiplican los denominadores de las dos operaciones y se resuelven todos los ejercicios. Ejemplo, 7/3 – 2/3 = 53
Suma de fracciones

Para realizar esta operación, se necesita saber si la suma posee el mismo denominador o si tiene uno diferentes, entonces, se aplican dos procedimiento distintos, en el primero se realiza una suma con el mismo denominador, en la cual se suman los numeradores, pero los denominadores se mantienen intactos, es decir, iguales. Se dice que esta es una de las formas más simples de resolver la operación.
Ahora, cuando se trata de denominadores diferentes, todo cambia, pues se necesita colocar un denominador común, es decir, el mínimo común múltiplo, luego, se multiplican los numeradores por el dígito que se haya escogido (el común múltiplo) para el denominador. De esta forma se simplifica la operación y se obtiene un resultado sencillo. Ejemplo, 7/10 + 10/10 = 17/10
División de fracciones
Esta también se conoce como operación de cociente y es aquella en la cual el numerador posee el resultado del numerador de la primera operación y el denominador de la segunda. Ahora, en el caso del denominador, este posee el producto del denominador de la primera operación y el numerador de la segunda. Ejemplo:
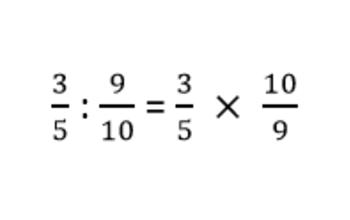
Simplificación de fracciones
Es aquella en la cual se divide tanto el denominador como el numerador por un mismo dígito, empezando la simplificación probando los dígitos primos, esto quiere decir que se empieza a probar la división del denominador y el numerador entre 2 mientras se tenga oportunidad, para después pasar al 3 y se repite el procedimiento hasta que no existan más divisores comunes. Ejemplo:

Otros usos de la palabra
Este término no tiene acepciones a nivel matemático, de hecho, es conocido y aplicado en diferentes culturas o ámbitos, entre ellos, los siguientes:
Fracciones religiosas
En la religión cristiana, este término es definido como aquel acto de dividir el pan mientras se está llevando a cabo la comunión, es decir, cuando se “recibe” el cuerpo de cristo.
Fracciones geográficas
Se trata de una subdivisión municipal existente en Italia, la cual corresponde a una entidad local menor, designada a un aglomerado de casas o simplemente asignado a una localidad pequeña, la cual está constituida dentro de un núcleo de casas aisladas de su sede principal.
Fracciones de un texto

Este término es empleado para hacer alusión a situaciones o conflictos sociales, políticos, culturales, económicos y ambientales, además, suelen hacer acto de presencia en las letras de canciones, guiones en diferentes programas televisivos, en la literatura, en aquellas frases célebres de los pensadores más famosos del mundo y que se convierten en un apoyo fundamental para desarrollar el pensamiento crítico.
Cada vez que este término aparece en alguna lectura, tiene un objetivo y es el de dejar una interpretación bastante profunda de la realidad que se vive, es por ello que se dice que funciona como un apoyo en la educación y en niveles genéricos.
Fracción parlamentaria
Se trata de un órgano de origen parlamentario creado para agrupar a los miembros de la asamblea de acuerdo a su afinidad partidista, es decir, a su partido político, pero también funciona para coordinar cada una de sus actuaciones y participar en la dirección de la institución política en cuestión.