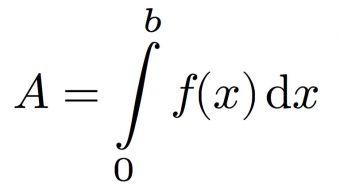Función

Qué es función

En términos generales, una función es aquél objetivo o propósito que tiene un individuo, un objeto, un proceso o una situación. Dicho de otra manera, es el «para qué» de un elemento, para qué está hecho o para qué se encuentra en determinado lugar. Como verbo “funcionar”, se refiere a la forma en la que un objeto, aparato, sistema o individuo interactúa o lleva a cabo su tarea o proceso, es decir, cómo funciona. Es un concepto que engloba de manera tangible todo lo relacionado a un proceso y a un objetivo, relacionando todas las acciones de su especie que podrán llegarse a necesitar.

Este término también se utiliza para todo aquello que se realiza enfocado hacia un fin específico, de ahí el término realizar algo “en función de”, refiriéndose a toda aquella acción que se lleva a cabo para el logro de un objetivo. Es una herramienta ideal para resolución de problemas, supone un concepto más determinado a una acción a realizar.

De igual manera, puede ser un tipo de exhibición o espectáculo. Por ejemplo, cuando vamos a ver una película, es a ver una función de cine, en la que un establecimiento desarrolla su servicio y las personas lo disfrutan. De igual manera el término puede estar asociado a un evento público o privado pero en el que se exponga algún arte.

Coloquialmente puede usarse este palabra para referirse a algún tipo de altercado o discusión que se dé entre dos o más personas y que se ha salido de proporción ocasionando un escándalo.

Su etimología proviene del latín «functio» que significa “ejecución o ejercicio de alguna facultad o el cumplimiento de un deber”. En nuestro idioma, el término puede concebirse como: la capacidad de un ser vivo, la tarea propia a la actividad, un acto masivo de carácter teatral o una relación entre dos o más elementos.

Qué es una función matemática

En el campo matemático es una herramienta didáctica y práctica con la que se definen situaciones o problemas a resolver. En matemática representa es la correspondencia entre dos conjuntos, de modo que un elemento del primer conjunto corresponde a otro elemento único del segundo conjunto, la cual se convertirá en una variable dependiente.

Este proceso debe cumplir con un esquema básico, y es en el que existe una relación entre dos formas, objetos o dos representaciones con un operador entre ellos, y cada elemento de cada parte debe mantener relación con todo dentro de la función.

Estas son una representación gráfica de los dos conjuntos. Este gráfico definirá algún resultado abstracto para cualquier otro ámbito, pero que dentro de un contexto y lógica matemática, tendrá sentido. Las funciones en este sentido, pueden representar el recorrido de una partícula.

Tipos de función matemática

De acuerdo a la correspondencia del primer conjunto con el segundo, existirán distintos tipos, las cuales pueden ser:

Función matemática

Es la relación de dependencia de una variable independiente (X), también llamado “dominio”; y una variable dependiente (Y), también llamado “codominio”, que en conjunto formarán lo que se llama “recorrido”, “ámbito” o “rango”.

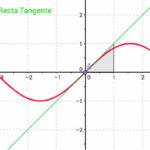
Existen tres maneras de expresar una función matemática, que son en forma gráfica donde se utiliza un sistema de cuatro cuadrantes determinados por los ejes X (horizontal) y Y (vertical) llamado plano cartesiano; en una expresión algebraica; y/o en una tabla de valores.

Usualmente para cada valor de X solamente le corresponderá un valor de la dependiente Y, a menos que se trate de otros tipos de funciones que le permitirán a la variable Y tener más de un valor de la variable X. Esto quiere decir, en funciones que la variable Y puede estar relacionada con más de un valor de la variable X. Estas son conocidas como suryectiva.

Función racional

Los números racionales son el cociente de dos números enteros, siendo su denominador distinto de cero. La función racional es aquella que está representada por una hipérbola (curva abierta de dos ramas opuestas) y está caracterizada por presentar asíntotas (recta a la que la función se aproxima de manera continua hacia el infinito sin llegar a coincidir). Su centro será el punto de corte de las asíntotas.

Algebraicamente, este tipo de función se representa de la siguiente manera:

• Donde G y L son polinomios y x es una variable. En este tipo, el dominio serán todos aquellos valores de x de la recta, de modo que no se anule el denominador, por lo que todos los números serán reales, excepto cuando x=0, siendo en este punto donde tendrá la asíntota vertical.
• De acuerdo al signo de G, si es mayor a 0, la hipérbola se encuentra en el primer y tercer cuadrante; y si es menor a 0 se encontrará en el segundo y cuarto cuadrante, siendo el centro de la hipérbola la coordenada 0, 0 (valor para x=0 x=0 y y=0).

Función lineal

Es aquella conformada por un polinomio de primer grado, que está representada por una línea recta en el eje cartesiano, la cual simbolizada algebraicamente, se verá así: F(x)= mx.

La letra m simboliza la pendiente de la recta, es decir, la inclinación de la pendiente respecto al eje de las abscisas (x). En el caso de que la x lleva valor positivo (mayor a 0), entonces la función sera creciente. Ahora, si la m presenta un valor negativo (menor a 0), la funcion será decreciente.

Función trigonométrica

Éstas son aquellas que se encuentran asociadas o relacionadas con una razón trigonométrica. Estas surgieron al observar un triángulo rectángulo y avistar que los cocientes entre las longitudes de dos de sus costados, solo estan sujetos al valor de los ángulos del triángulo.

Para definir las funciones del ángulo alpha de un triángulo rectángulo, se deben definir la hipotenusa (lado opuesto al ángulo recto, siendo el lado más grande), el cateto opuesto (el lado opuesto a dicho ángulo alpha) y el cateto adyacente (el lado adyacente al ángulo alpha).

Las seis funciones trigonométricas básicas que existen son:

1. Seno, que es la relación entre la longitud del cateto opuesto con la de la hipotenusa, siendo:

2. Coseno , es la relación entre la longitud del cateto adyacente y de la hipotenusa, por lo que:

3. Tangente , relación entre la longitud del cateto opuesto y el adyacente, siendo:

4. Cotangente , relación entre la longitud del cateto adyacente y el opuesto:

5. Secante , es la relación entre la longitud de la hipotenusa y del cateto adyacente:

6. Cosecante , relación entre la longitud de la hipotenusa y el cateto opuesto, siendo:

Función exponencial

Es aquella donde su variable independiente X aparece en el exponente, con base en su constante a, expresada de la siguiente manera: f(x) = aˣ.

En donde a es un número real positivo mayor a 0 y diferente de 1. Si la constante a es mayor que 0 pero menor que 1, entonces la función es decreciente; mientras que si es mayor que 1, entonces la función será creciente. Este tipo también viene expresado como exp(x) y es considerada como la inversa de la función logarítmica.

Las propiedades de la función exponencial son: exp(x+y) = exp(x).exp(y); exp(x-y) = ; y exp(-x) =.

Función cuadrática

También denominada como función de segundo grado, Es aquella donde su exponente no será mayor a 2. Su fórmula se expresa de la siguiente manera: f(x) = ax 2 + bx + c.

La forma gráfica en el plano cartesiano de este tipo de herramienta matemática es una parábola, y se abrirá hacia arriba o hacia abajo dependiendo del signo o valor de a: si la constante a es mayor a 0, la parábola abrirá hacia arriba; y si es menor que 0, abrirá hacia abajo.

Esta puede presentar una, dos o ninguna solución, que va a significar uno, dos o ningún corte con el eje de abscisas (eje X).

Función logarítmica

Está determinada por un logaritmo (exponente al que hay que elevar la base para obtener dicho número). Su fórmula algebraica está conformada de la siguiente manera: logb y = x

Donde a es un número real positivo mayor a 0 y distinto de 1. Cuando a es menor a 1 y mayor a 0, la función logarítmica será decreciente; mientras que si es mayor a 1, será creciente. La función logarítmica es la inversa de una función exponencial. Su dominio está conformado por números reales positivos y su recorrido son números reales.

Función polinomial

También llamada polinómica, es una relación en la que para cada valor de X se le asigna un valor único como resultado de sustituirlo en un polinomio asociado a la función. Se expresa algebraicamente de la siguiente manera: 4x + 5y + 2xy + 2y +2.

Existen distintos tipos de relaciones polinómicas según su grado polinomial, las cuales son son:

• Constantes, que son aquellas de grado 0, siendo 0 el coeficiente de x, sin depender de la variable independiente X: donde a es una constante.
• De primer grado, que comprenden un escalar que multiplica la variable X más una constante, siendo X1 su mayor exponente, de manera que quede así: donde m es la pendiente y n la ordenada (valor desde 0 al punto de corte en el eje Y). De acuerdo al valor de m y n existen tres tipos de funciones polinomiales de primer grado: afines (que no pasan por el origen), lineales (la ordenada es 0 y m es la pendiente distinta a 0) e identidad (cada elemento de X es igual a su valor en Y).
• Cuadráticas, de grado 2, ya explicadas previamente.
• Cúbicas, que son de grado 3, por lo que su mayor exponente será X3, de esta forma: donde a es distinto de 0.

Función en cálculo

Es un conjunto de elementos cuyo valor corresponde a un único valor de un segundo conjunto de elementos. Dicha relación se ilustrará a través de un diagrama en el que se señalarán los puntos de intersección de dichos valores correspondientes, los cuales, en su totalidad, formarán un gráfico que representará un recorrido.

Para comprender el significado de función en cálculo se deben tomar en cuenta los siguientes conceptos:

• Dominio: Son todos los valores que puede tomar la variable independiente X, de tal modo que la variable dependiente Y sea un número real.
• Rango: También llamado contradominio, es el grupo de todos los valores que puede tomar una función y dependen de los valores de X.

Otros tipos de función

En diferentes contextos, se pueden concebir otros tipos de funciones, entre los que se pueden destacar:

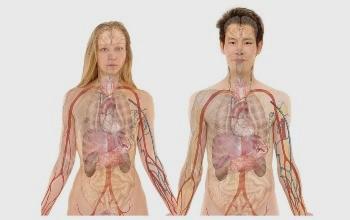
Funciones del cuerpo

El cuerpo humano realiza incontables labores o funciones, las cuales pueden ser vitales y no vitales. Las funciones no vitales del cuerpo humano son aquellas que, aunque son importantes, no son esenciales para mantener vivo al organismo, como por ejemplo el movimiento, ya que una persona puede permanecer toda su vida sin caminar.

Las funciones vitales son aquellas sin las cuales no sería posible el funcionamiento del cuerpo y, por lo tanto, la vida en el mismo. Éstas, también denominadas vegetativas, son:

• Nutrición: En esta intervienen el aparato digestivo, circulatorio, respiratorio y excretor. Para este último, intervienen otras funciones, como la función del hígado, de las glándulas sudoríparas, de los pulmones y de los riñones.
• Relación: Aca se involucran el sistema endocrino y el sistema nervioso. El sistema nervioso, a su vez, se divide en el sistema nervioso central (encéfalo y médula espinal) y sistema nervioso periférico (sistema nervioso somático: nervios aferentes y eferentes; y sistema nervioso autónomo: sistema nervioso simpático y parasimpático).
• Reproducción: Intervienen los aparatos reproductivos masculino y femenino. Esta si bien no es vital para que un solo individuo se mantenga vivo, sí lo es para la perpetuidad de la especie.

En el cuerpo existen muchos elementos que tienen una misión determinada. Las funciones de las proteínas, por ejemplo, son estructurales, enzimáticas, hormonales, reguladoras, defensivas, de transporte, entre otras. La función de los lípidos es similar a la de las proteínas, ya que de igual forma cumplen con funciones de reserva, estructurales y reguladoras. La función del cerebro son las de controlar el sistema nervioso central, es responsable del pensamiento y del control del cuerpo. En una célula, la función del núcleo es la de preservar y controlar los genes y actividades propias de la misma.

Funciones del lenguaje

Cuando se trata de comunicar un mensaje dentro del lenguaje, se realiza con una intencionalidad y un objetivo, del cual dependerá qué elemento que interviene en la misma tendrá un mayor protagonismo. Estos elementos son: emisor, receptor, mensaje, canal, contexto y código. De acuerdo a esto, el proposito del lenguaje es:

• Representativa o referencial: permite transmitir un mensaje de manera objetiva, informando hechos o ideas, siendo el contexto temático el elemento predominante.
• Expresiva: Esta permite expresar sentimientos, deseos u opiniones desde un punto de vista subjetivo, siendo el emisor el elemento predominante.
• Conativa o apelativa: Su objetivo es la de influir en el comportamiento del receptor para inducir una reacción o que haga algo. Su elemento predominante es el receptor.
• Fática: consiste en extender, crear o interrumpir la comunicación. Su elemento predominante es el canal.
• Metalingüística: tiene por objetivo la de utilizar el lenguaje para hacer referencia al mismo lenguaje, siendo su elemento predominante el código (lenguaje).
• Poético: Se presenta en textos literarios, la cual busca alterar el lenguaje cotidiano con un objetivo, siendo importante la forma expresiva. Su elemento predominante es el mensaje.

Funciones en Excel

En el contexto informático, específicamente para aplicaciones y herramientas de trabajo tales como Excel, es una fórmula predeterminada que sirve para realizar cálculos a través de valores o argumentos que el usuario provea al mismo en un orden específico. Estas permiten al usuario evitar realizar dichos cálculos a mano y uno por uno.

Para entender cómo trabajan estas fórmulas en Excel, es necesario definir la sintaxis de la misma, la cual se conforma de la siguiente manera: la utilización del signo igual (=), la función que se realizará (si es adición, sustracción, etcétera) y finalmente los argumentos o datos que completarán la fórmula. Estos últimos son suministrados por el usuario, los cuales pueden ser rangos de celdas, texto, valores, comparaciones de celdas, entre otros.

La aplicación cuenta con una gran gama de herramientas para facilitar y complementar el trabajo de una persona, y se agrupan en: funciones de búsqueda y referencia, de texto, lógicas, de fecha y hora, de base de datos, matemáticas y trigonométricas, financieras, estadísticas, de información, de ingeniería, de cubo y web.

Función pública

Este concepto está relacionado con las labores y responsabilidades que le son asignadas a una institución, organismo, entidad, fundación o corporación, que son de interés y carácter público, para trabajar enfocándose hacia la prestación de un servicio de interés local, regional o nacional.

Usualmente dichos organismos son pertenecientes al Estado de una nación, quienes serán los encargados del ejercicio de dicha actividad pública, también denominada administración pública. Sus empleados son denominados como funcionarios o funcionarios públicos.