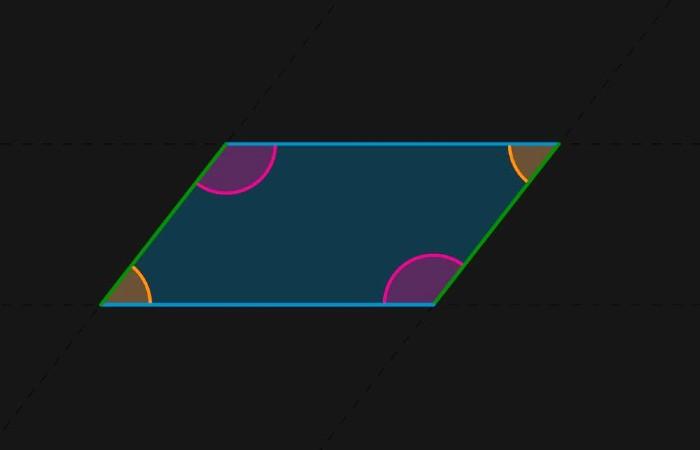
Qué es un paralelogramo
Es un polígono que consta de cuatro lados, cuya condición que debe cumplir es que sus lados opuestos tengan la misma longitud y sean paralelos entre sí. En la vida diaria, es posible que las personas se topen a menudo con estas figuras, ya que son incontables los objetos que pueden tener esta forma, ya sea un libro, una regla, un escritorio, una tabla, entre muchos otros.
Este es de gran utilidad para disciplinas como la ingeniería, arquitectura y la carpintería. Igualmente sirve para otros cálculos, por ejemplo, para hallar la suma de dos vectores, a lo que se conoce como método del paralelogramo.
La etimología de la palabra se encuentra compuesta por el latín parallelos cuyo origen se encuentra en el griego «para«, que significa “junto a”, y «alelon«, que significa “mutuamente”. Por otro lado, el sufijo grama, significa “escrito” o “dibujo”.
Características y propiedades del paralelogramo
Entre las características o propiedades, se tienen las siguientes:
- Sus lados opuestos deben tener la misma longitud.
- Los mismos deben ser paralelos entre sí.
- La suma de sus ángulos internos es de 360 grados.
- Todo paralelogramo es un cuadrilátero, pero no todo cuadrilátero es un paralelogramo.
- Los ángulos opuestos son iguales.
- Sus diagonales se dividen en dos partes iguales por el punto donde intersectan.
- La suma de los cuadrados en sus diagonales es igual a la suma de los cuadrados de sus lados.
- Sus diagonales los dividen en triángulos iguales.
- Las bisectrices de sus lados opuestos son paralelas, y las de sus lados adyacentes forman un ángulo recto.
Clasificación de los paralelogramos
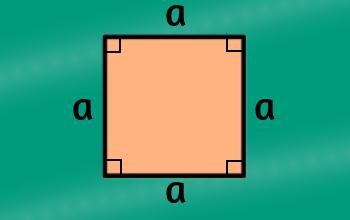
Cuadrado
Son paralelogramos cuyos cuatro lados son iguales, al igual que sus ángulos. Este cumple con la particularidad de ser cuadrilátero, rectángulo y rombo al mismo tiempo, ya que sus cuatro ángulos son iguales y rectos.
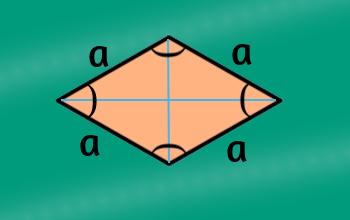
Rombo
Este es un polígono, cuadrilátero y paralelogramo, en los que sus cuatro lados son iguales, sus lados opuestos entre sí, pero sus ángulos no son necesariamente rectos. Sus ángulos opuestos sí serán y sus diagonales son perpendiculares entre sí.
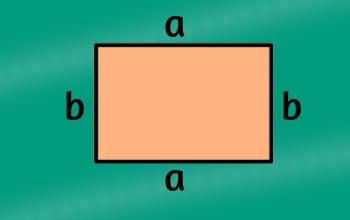
Rectángulo
Es un polígono, cuadrilátero y paralelogramo, cuyos lados opuestos son iguales y paralelos y sus ángulos son rectos.
Romboide
Es un cuadrilátero cuyos lados opuestos son iguales entre sí, al igual que sus ángulos opuestos. Sus diagonales no son perpendiculares como el caso del rombo, ya que sus lados adyacentes son distintos.
Fórmulas del paralelogramo
paralelogramo, es necesario que se multiplique la altura (h) por la base (b). |
su altura h=3 cm, se tendría que: Área = 5.3 = 15 cm2 |
||
iguales, pero esta es de menor longitud que sus lados; los rectángulos tienen dos alturas de acuerdo a la base que se tome, si la base es menor, la altura es mayor y viceversa; y en el romboide se tienen dos alturas, las cuales no coinciden con ninguno de sus lados. |
b=6 cm, y su área A=24 cm2, se tendría que: h=24/6 = 4 cm |
||
cada extremo opuesto de estos cuadriláteros, los cuales se cortarán en sus puntos medios. Estas serán perpendiculares únicamente en el caso de los cuadrados y los rombos; y si son iguales, se trata de un rectángulo o cuadrado. La fórmula utilizada para su cálculo es la ley del paralelogramo |
|||
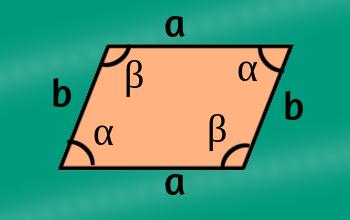
suman 360º, dispuestos así: sus ángulos opuestos son congruentes; mientras que sus ángulos adyacentes son suplementarios (ambos sumarán 180º). Por lo tanto: α=δ y β=ε; además, β=180º-α o α=180º-β. |
|||
paralelogramo |
Ley del paralelogramo
Permite establecer relación entre los lados y diagonales del mismo. Dicha ley establece que al sumar los cuadrados de las longitudes de los 4 lados, es proporcional a la suma de los cuadrados de la longitud de cada diagonal.
Su fórmula está dada por 2.(a2+b2)=D12+D22.