Qué es un Triángulo Equilátero
Este término hace referencia a un polígono de tipo regular, porque todos los ángulos de un triángulo equilátero son iguales, al igual que la longitud de sus lados. De acuerdo a la geometría, estos triángulos también son considerados como equiangulares.
Etimológicamente el triángulo equilátero se compone de dos palabras derivadas del latín. Triángulo que contempla el prefijo tri que significa tres y el sustantivo angulus, que es equivalente a córner. Equilátero proviene de aequilaterus y se forma de dos palabras aequus, que es sinónimo de igual, y lateralus, que significa lado.
Por otra parte, dependiendo de las características del polígono en cuanto a sus ángulos y lados, puede ser aplicada la terminología triángulo equilátero, isósceles y escaleno. Por ejemplo, el triángulo isósceles se caracteriza por poseer al menos dos lados con igual longitud y dos ángulos internos agudos iguales, de ahí que un triángulo con todos sus ángulos y lados iguales podría ser un caso especial de este y se puede calificar como triángulo equilátero isósceles. En cambio, un triángulo escaleno es aquel que ninguno de sus lados es igual, en consecuencia, no se puede considerar isósceles.
Características de un triángulo equilátero
Para describir las características de este tipo de triángulo es necesario explicar algunos conceptos.
- Simetría: en geometría un objeto es simétrico cuando al efectuar una transformación, ya sea división, rotación, reflexión o traslación este no varía.
- Vértice: se refiere al punto de unión de dos rectas o segmentos.
- Mediana: en los triángulos se define como la recta que une a un vértice con el punto medio del lado opuesto a éste. Así mismo, el punto de corte de todas las medianas del triángulo se denomina baricentro.
- Mediatriz: es la recta trazada perpendicularmente por el punto medio de un segmento.
- Bisectriz: es la recta que divide al ángulo interno de un triángulo en dos partes iguales y que pasa a través del vértice hasta llegar a su lado opuesto. El punto de corte de las tres bisectrices en un triángulo se le denomina incentro.
- Altura: se define como la recta que se traza desde el vértice de un triángulo hasta el lado opuesto de este perpendicularmente. El punto donde se cruzan las tres alturas se llama ortocentro.
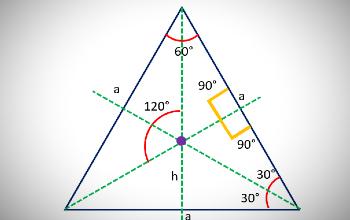
Al examinar sus características tenemos:
- Su mediatriz, mediana, bisectriz y altura, coinciden en la misma recta, generando que el baricentro, incentro y ortocentro coinciden en un mismo punto central.
- Cuenta con tres ejes de simetría y cada uno de ellos pasa a través de un vértice hasta el punto medio del lado opuesto dividiéndolo en partes iguales o triángulos rectángulos, en los que uno de sus ángulos mide 90 grados.
- La simetría también se verifica tomando el baricentro como centro rotativo, las rotaciones 0, 120, y 240 grados llevan la figura sobre sí misma.
- Otra particularidad es que son congruentes, ya que todos los ángulos de un triángulo equilátero son iguales.
- Son semejantes porque al compararlo con otro equilátero, sus lados son proporcionales y sus ángulos son los mismos.
Calcular área
Para calcular el área de un triángulo se multiplica la base por su altura y se divide entre dos. La altura de un triángulo equilátero (h), se puede determinar con el teorema de Pitágoras el cual consiste en relacionar los catetos de un triángulo rectángulo con su hipotenusa, donde la hipotenusa es el lado opuesto al ángulo de 90 grados y los catetos son los segmentos que forman el ángulo recto.
Para aplicar este teorema y calcular el área de un triángulo equilátero se pasa una recta desde un vértice hasta el punto medio de su lado opuesto y se obtiene un triángulo rectángulo, de manera que la altura es la raíz cuadrada de 3 por la hipotenusa entre 2 y esta será sustituida en la fórmula del área de un triángulo.
Para la demostración se utilizan las siguientes imágenes del triángulo equilátero:
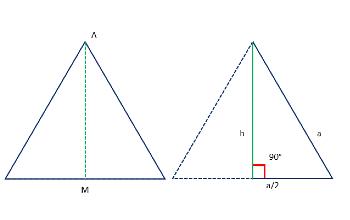
Tomando en cuenta el teorema de pitágoras:
La fórmula de triángulos equiláteros para área es:
Calcular perímetro
Dado que los tres lados del triángulo equilátero son iguales, el perímetro de este tipo de triángulos se puede calcular multiplicando la longitud de uno de sus lados por tres.
Ecuaciones del triángulo equilátero
El siguiente ejemplo permitirá comprender cómo utilizar la fórmula de un triángulo equilátero.
- Calcular el perímetro y área de un triángulo equilátero donde cada lado mide 5 cm.
- Para el área se tiene:
Ejemplos de triángulos equiláteros

Los triángulos son de utilidad en la vida cotidiana, y se encuentran con más frecuencia de lo que se piensa. Es una figura que no se puede deformar y tiene la capacidad de formar otros polígonos. Ejemplos de ello son:
- En geometría, un triángulo equilátero puede permitir formar otros polígonos: un rombo a través de la unión de dos equiláteros, un trapecio isósceles por la unión de tres triángulos conectados
- Saber calcular el área de este tipo de triángulo permite formar triángulos rectángulos, los cuales se usan para realizar diferentes cálculos matemáticos. Estos se aplican para el diseño arquitectónico de las pirámides, puentes y edificios. También, en la física se utiliza para calcular la altura máxima, distancias lineales, verticales o horizontales.
- En la agricultura, para construir soportes para las plantas.
- Los carteles de tránsito son otro ejemplo donde se utilizan triángulos equiláteros como: señales para ceder el paso, cuidado, etc.