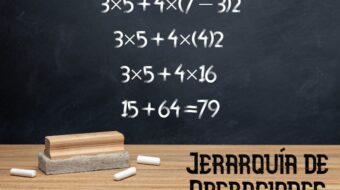Qué es el álgebra
Es la rama que pertenece a la matemática, la cual permite desarrollar y resolver problemas aritméticos a través de letras, símbolos y números, que a su vez simbolizan objetos, sujetos o grupos de elementos. Solucionando así operaciones que contienen números desconocidos, llamados incógnitas.
Este campo ha permitido contabilizar de forma abstracta y genérica, pero también ha logrado resolver cálculos más complejos, que han sido desarrollados por algunos matemáticos y físicos del campo como sir Isaac Newton (1643-1727), Leonhard Euler (1707-1783), Pierre de Fermat (1607-1665), entre otros.
Según la historia del álgebra, Diofanto de Alejandría (quien vivió entre los siglos III y IV) fue el padre de esta rama, ya que publicó una obra llamada Arithmetica, donde realiza la implementación de los símbolos universales para la representación de una incógnita dentro de las variables del problema a resolver.
El origen de la palabra “álgebra”, proviene del árabe “alǧabru” y significa “restauración” o “reconocimiento”. De igual forma tiene su significado en el latín, que corresponde a “reducción”, y, aunque no son términos idénticos, significan lo mismo.
Como herramienta adicional para el estudio de esta rama, se puede contar con la calculadora algebraica, que son calculadoras que pueden graficar las funciones algebraicas y resolver diversos problemas, ya sean suma, resta, divisiones, fracciones algebraicas, etc.
Dentro del álgebra se encuentra el concepto de término algebraico, que es el producto de un factor numérico de al menos una variable de letra.
Características del álgebra
Esta área presenta propiedades específicas que le permiten la resolución de los problemas aritméticos.
Lenguaje y expresiones algebraicas

- Se denomina lenguaje y expresión a los signos matemáticos conformado por constantes enteras, variables y operaciones algebraicas.
- Las operaciones que conforman su lenguaje, son: la adición o suma algebraica, la sustracción o resta, la multiplicación, la división, la potenciación (multiplicación de un factor varias veces) y la radicación (operación inversa de la potenciación).
- Los signos utilizados son: suma (+) y la resta (-), en la multiplicación se sustituye la equis (x) por un punto (.) o pueden representarse con signos de agrupación (ejemplo: c.d y (c)(d) equivalen al elemento “c” multiplicado por el elemento “d” o cxd) y en la división algebraica se utilizan dos puntos (:).
- Sus signos de agrupación son: los paréntesis (), los corchetes [], las llaves {} y las rayas horizontales.
- Sus signos de relación, son entre los más usados el de igual a (=), mayor que (>) y menor que (<).
- También incluye los números reales (racionales, que incluyen los positivos, negativos y el cero; y los irracionales, que son aquellos que no pueden representarse como fracciones) o complejos, que son parte de los reales, formando un cuerpo algebraicamente cerrado.
- Existen expresiones de dos tipos: los monomios, que son los que tienen un único sumando; y los polinomios, que tiene dos (binomios), tres (trinomios) o más sumandos.
Funciones algebraicas
Se clasifican en: racional, irracional y de valor absoluto.
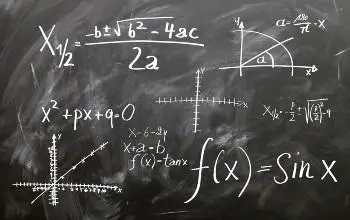
- Las funciones racionales enteras, son aquellas expresadas en donde “P” y “Q” representan dos polinomios y “x” la variable, en donde “Q” es distinto al polinomio nulo, y la variable “x” no anule al denominador.
- Las funciones irracionales, en las que la expresión f(x) representa a un radical, de esta manera: si el valor de “n” es par, el radical será definido para que g(x) sea mayor e igual a 0, y además debe indicarse el signo del resultado, ya que sin éste, no podría hablarse de una función, dado que para cada valor de “x” se tendrían dos resultados; mientras que si el índice del radical es impar, no resulta necesario esto último, pues el resultado sería único.
- Las funciones de valor absoluto, donde el valor absoluto de un número real será su valor numérico dejando a un lado su signo. Por ejemplo, 5 vendrá siendo el valor absoluto tanto de 5 como de -5.
Álgebra lineal
Este término algebraico es el que estudia los conceptos de vectores, matrices, sistemas de ecuaciones algebraicas lineales, espacios vectoriales, transformaciones lineales y las matrices.
Su utilidad varía desde el estudio del espacio de las funciones, que son aquellas que se definen por un conjunto X (horizontal) a un conjunto Y (vertical) y se aplican para espacios vectoriales o topológicos; las ecuaciones diferenciales, las cuales relacionan a una función (valor que depende del segundo valor) con sus derivadas (razón de cambio instantánea que hace variar el valor de una función determinada); la investigación de operaciones, que aplica métodos analíticos avanzados para tomar decisiones acertadas; hasta la ingeniería.
Uno de los ejes principales se encuentra en los espacios vectoriales, conjunto de vectores (segmentos de una recta) y un conjunto de escalares (números reales, constantes o complejos, que poseen magnitud, pero no la característica vectorial de dirección).
Los principales espacios vectoriales de dimensión finita, son tres:
- Los vectores en Rn, que representan coordenadas cartesianas (eje horizontal X y eje vertical Y).
- Las matrices, que son sistemas rectangulares de expresiones (representadas por números o símbolos), se caracterizan por una cantidad de filas (usualmente representada por la letra “m”) y una cantidad de columnas (representada por la letra “n”), y se usan en ciencias y la ingeniería.
- El espacio vectorial de polinomios en una misma variable, dado por polinomios que no superan el grado 2, poseen coeficientes reales y se encuentran sobre la variable “x”.
Álgebra de Baldor
Se refiere a una obra desarrollada por el matemático, profesor, escritor y abogado Aurelio Baldor (1906-1978), la cual fue publicada en el año 1941. Este profesor cubano, en su aporte reseña 5.790 ejercicios equivalentes a un promedio de 19 ejercicios por prueba.

El contenido de la obra se encuentra dividido en 39 capítulos y un apéndice, que contiene tablas de cálculos, cuadro de formas básicas de descomposición de factores y tablas de raíces y potencias.
Este libro es la iniciación por excelencia para los estudiantes de secundaria dentro del mundo algebraico, siendo el libro más consultado y completo sobre la materia, por contener una explicación clara sobre los conceptos y sus ecuaciones algebraicas.
Álgebra booleana
El álgebra booleana es un sistema matemático creado por el inglés George Boole (1815-1864) para representar cualquier tipo de circuito lógico a modo de ecuaciones algebraicas. Boole creó un grupo de leyes y reglas para realizar operaciones algebraicas en el ámbito electrónico, gracias a esto se le considera uno de los precursores de las ciencias de la computación.
En los problemas lógicos y filosóficos, las leyes que Boole desarrolló permitieron simplificarlos en dos estados, que son el estado verdadero o el estado falso, y a dichas conclusiones se llegaban mediante una vía matemática, como contactores y relés. Tales estados tienen una representación numérica 1 y 0, donde el 1 representa lo verdadero y el 0 a lo falso, lo que hace más fácil su estudio.
Esta rama permite simplificar los circuitos lógicos o de conmutación lógica dentro de la electrónica digital; también a través de ella, se pueden realizar cálculos y operaciones lógicas de los circuitos de una forma más expresa.
En el campo booleana existen tres procedimientos fundamentales, que son:
- El producto lógico, la puerta AND o función intersección.
- La suma lógica, puerta OR o función unión.
- La negación lógica, puerta NOT o función complemento.
Y también, funciones auxiliares:
- Negación del producto lógico, puerta NAND.
- Negación de la suma lógica, puerta NOR.
- Suma lógica exclusiva, puerta XOR.
- Negación de la suma lógica exclusiva, puerta XNOR.