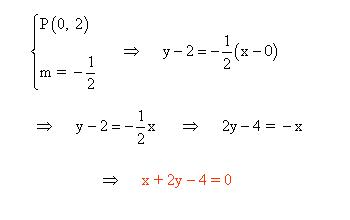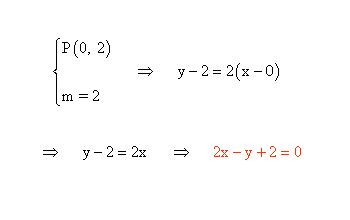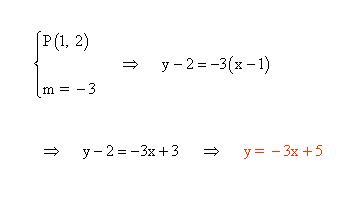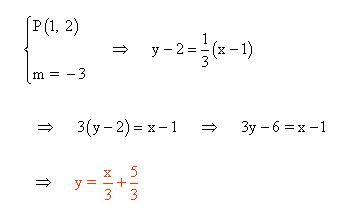Que es bisectriz
Bisectriz es una semirrecta que se caracteriza por cortar un ángulo en dos partes iguales. Es un lugar geométrico que tiene su origen en el vértice del ángulo y culmina en la división del ángulo.
Es importante resaltar que se denomina lugar geométrico al grupo de puntos colocados a un lado del punto fijo de la recta, ésta tiene un punto de origen y como todas las rectas se expande hacia el infinito. Del mismo modo el punto de la bisectriz será de igual distancia a las dos rectas que forman el ángulo. Debido a su correlación, cuando dos rectas se entrelazan forman cuatro ángulos.
La bisectriz de un triángulo se refiere al punto de intersección entre las tres rectas bisectrices de cada uno de los respectivos ángulos internos. Este punto se conoce con el nombre de incentro del triángulo, el cual concuerda con el centro de la circunferencia inscrita en dicho triángulo, es decir, aquella circunferencia que el tangente con cada uno de los tres lados del polígono. Existen tres bisectrices (Ba, Bb,Bc) y se calcula la longitud de las bisectrices mediante el teorema de la bisectriz.
Los términos circuncentro, incentro, bisectriz y mediatriz son recurrentes cuando se habla de un triángulo y aunque se relacionan existen diferencias entre ellos. El incentro es la intersección de las rectas bisectrices de los ángulos del triángulo, mientras el circuncentro corresponde con la intersección de las rectas mediatrices. Estos puntos coinciden sólo cuando los triángulos son equiláteros.
El término “Bisectriz” tiene un origen latino, refiriéndose a “que corta en dos partes iguales». Generalmente se usa en la geometría, aplicando figuras geométricas con bisectrices.
Características de la bisectriz
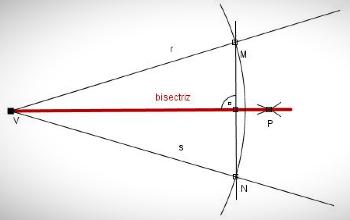
En esta vertiente se mencionan las características que presenta la bisectriz:
- Posee dos propiedades, las cuales son: La bisectriz es el eje de simetría del ángulo y sus puntos son equidistantes a los dos lados del ángulo.
- Las bisectrices son el origen o lugar geométrico de puntos equidistantes. Debido a esto tienen una distancia idéntica a las de la semirrecta que forman el ángulo.
- La bisectriz de un ángulo cuenta con la posibilidad de formar dos ángulos con un lado en común.
- Cuando dos rectas se cruzan entre sí, determinan cuatro ángulos de forma consecutiva y sus bisectrices, forman cuatro ángulos rectos siendo todos consecutivos.
- Las bisectrices se calculan mediante una serie de pasos que consiste en buscar primero el punto de corte de las rectas, para luego hallar los vectores directores de la bisectriz y por último determinar la bisectriz.
- Se calcula para conocer el punto de corte de los ángulos a partir del vértice.
Trazado de bisectriz
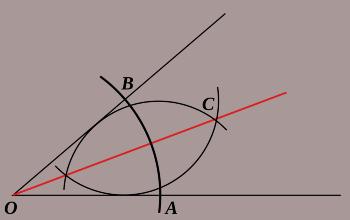
El trazado o técnica de bisectriz consiste en un procedimiento que se lleva a cabo mediante una serie de pasos, los cuales se presentan a continuación:
- Para comenzar se traza un ángulo.
- Los ángulos se deben nominar con las letras A, O y B, siendo O el vértice.
- Con la ayuda de un compás, se realiza el centro en el vértice 0.
- Se escoge cualquier radio para cortar. Los puntos de corte resultantes se nombran P y Q.
- Con el compás se realiza centro en los puntos P y Q y luego se trazan dos arcos que tengan el mismo radio suficientemente grande como para que se crucen. Esto genera el punto C.
- Después de una regla, se traza una recta que une al vértice 0 con el punto C y de esta manera se forma la bisectriz.
Ejercicios de bisectriz
A continuación se presentan algunos ejercicios de bisectriz resueltos con la explicación correspondiente:
- Determina la ecuación de la recta ´´r´´ que pasa por el punto (2, 1) la cual, junto con la recta s: y = 2x – 1 genera un ángulo de 45º.
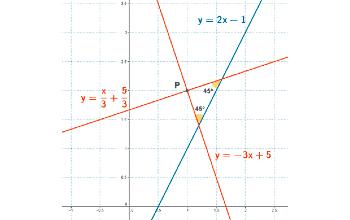
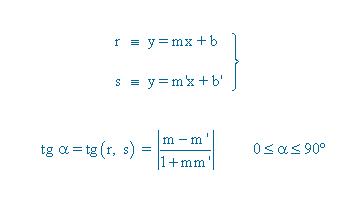
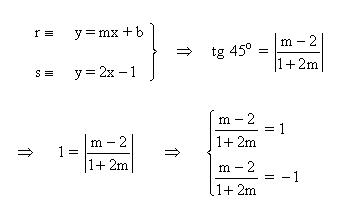
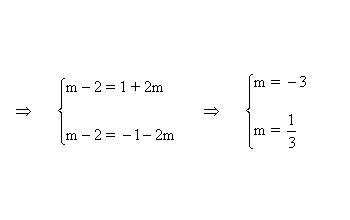
Por último aplicar la ecuación punto pendiente que pasa por en punto (2,1):
- Determina las ecuaciones de las siguientes rectas, las cuales pasan por el punto de intersección de las rectas y = x + 2 y 3x + y = 2 y crean un ángulo de 45º con la segunda de ellas.
Lo primero que se hace es determinar el punto de corte de ambas rectas:
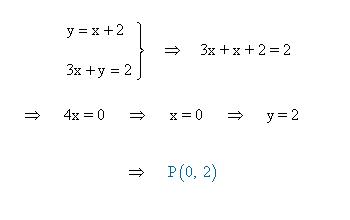
Luego calculamos el ángulo que forma la recta que nos piden con la segunda con la fórmula de la tangente del ángulo que forman dos rectas:
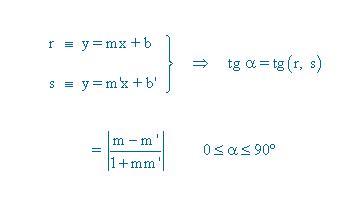
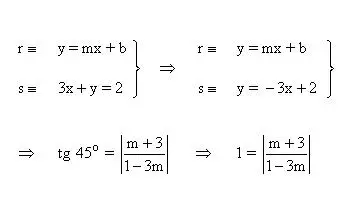
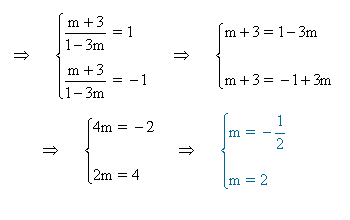
Por último, se realiza la ecuación punto pendiente correspondiente al punto (0,2):