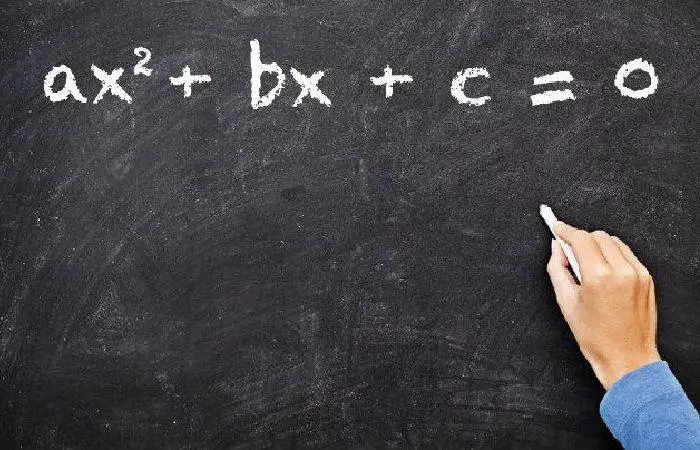Ecuaciones de Segundo Grado

Tabla de contenido

Qué son las ecuaciones de segundo grado

Son operaciones matemáticas integradas por elementos denominados términos sumadas algebraicamente e igualada a cero. Cada término se compone de un coeficiente y la …

La ecuación de segundo grado también denominada ecuación cuadrática, es una fórmula matemática igualada a cero y que depende de una variable. Es representada por tres términos, uno con la variable elevada a la dos ( $https://latex.codecogs.com/svg.image?x^{2}$ ), denominada cuadrático, otro con la variable con exponente uno (X) denominado lineal y un término independiente sin variable. Para resolver ecuaciones de segundo grado se aplica la resolvente, por medio de la cual se obtienen dos valores denominados raíces.

Tabla de contenido

Qué son las ecuaciones de segundo grado

Son operaciones matemáticas integradas por elementos denominados términos sumadas algebraicamente e igualada a cero. Cada término se compone de un coeficiente y la variable con los grados exponenciales 0, 1 y 2. El término con la variable elevada a la potencia cero se denomina término independiente (por no depender de la variable), mientras que el coeficiente del término cuadrático nunca puede ser cero.

Su resolución se obtiene a partir de la aplicación de la fórmula resolvente, generando dos posibles valores para la variable que se denominan raíces, las cuales pueden ser reales o imaginarias.

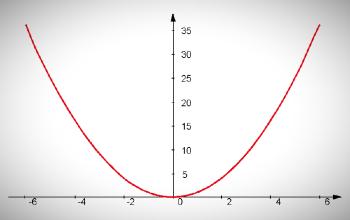
Estas ecuaciones pueden ser representadas por medio de un polinomio cuadrático y pueden ser interpretadas mediante una gráfica en forma de parábola.

Al ser una palabra compuesta por dos términos, las ecuaciones cuadráticas tienen dos significados:

Por una parte, el término ecuación se deriva del latín aequatío, cuyo significado es nivelación o repartición de algo en partes iguales.

En cuanto al segundo término, las ecuaciones algebraicas fueron denominadas cuadráticas porque la variable es elevada al cuadrado y no a una potencia mayor. La etimología de esta segunda palabra también está relacionada con el despeje de la incógnita: para resolverlas es necesario aplicar la raíz cuadrada para hallar los valores de la variable.

Características de las ecuaciones de segundo grado

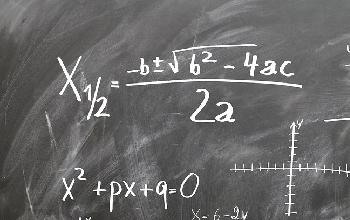
Aunque existen diferentes tipos de ecuaciones, las características principales de la fórmula de las ecuaciones de segundo grado son las siguientes:

Es un polinomio cuadrático.
Se compone de tres términos sumados algebraicamente.
Se representa igualando la suma algebraica de los términos a cero.
Cada término se compone de un coeficiente y la variable con potencias 0, 1 y 2.
El coeficiente del término cuadrático nunca puede ser igual a cero.
Se puede factorizar en un producto notable.
Cuando alguno de los coeficientes de los términos no cuadráticos es igual a cero, se considera incompleta.
Su solución se obtiene a través de la aplicación de la ecuación resolvente.
Su solución consta de dos valores posibles que puede tomar la variable, se denominan raíces y pueden ser tanto reales como imaginarias.
Esta ecuación representa gráficamente una parábola. Si el coeficiente del término cuadrático es negativo, la parábola asociada a la ecuación será cóncava, de lo contrario será convexa.
Si la ecuación se factoriza en un producto notable, los parámetros corresponden con las coordenadas del vértice de la parábola asociada.
Cuando las raíces son iguales, la coordenada en Y del vértice de la parábola es cero.
Cuando la parábola no corta al eje de las X‘s se dice que no tiene raíces reales o solución.

Ecuación de Segundo Grado - Parábola con vértice en el origen

Para elaborar un problema de ecuaciones de segundo grado se recomienda que las raíces de la solución sean reales, pudiendo ser enteras o racionales. Si el objetivo es graficar la ecuación, no se pueden tener como resultado raíces imaginarias (raíces cuadradas de números negativos) y es inconveniente tener raíces irracionales.

Para ello resulta útil crear la ecuación a partir de un producto notable. Donde se escogen cualquier número entero. Ejemplo:

$\left ( x + 4 \right )\left ( x + 2 \right )= 0$

Fórmula de las ecuaciones de segundo grado

Su representación general viene dada con la fórmula:

$ax^{2}+bx+c=0$

Donde a, b y c son los coeficientes que multiplican a las variables y las incógnitas son las equis.

Por otra parte, la resolución de las ecuaciones de segundo grado se obtiene a través de la aplicación de la resolvente:

$x_{1,2}=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}$

Donde a, b y c son los coeficientes de la ecuación cuadrática.

El termino b² – 4ac dentro de la raíz se denomina determinante, se representa con la letra griega delta Δ y a través del valor que toma se puede deducir el resultado de la ecuación.

Si Δ > 0 la ecuación tiene dos raíces reales, es decir, dos soluciones.
Si Δ = 0 la ecuación tiene una sola raíz, es decir, una solución.
Si Δ < 0 la ecuación tiene raíces imaginarias, es decir, no tiene solución.

Clasificación

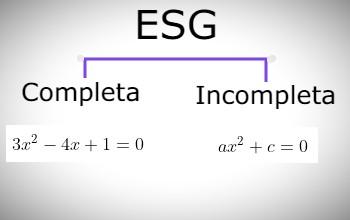
Ellas pueden ser clasificadas en dos tipos: ecuaciones de segundo grado completas y ecuaciones de segundo grado incompletas.

Completas

Son aquellas en las que ninguno de sus términos tiene coeficiente cero, es decir, tienen un término de segundo grado (elevado al cuadrado), un término lineal (es decir, «en x») y un término independiente, es decir, un número sin x. Un ejemplo de una ecuación de este tipo es la siguiente, ejemplo:

Dada la siguiente ecuación

$3x^{2}-4x+1=0$

Donde a = 3, b = 4 y c = 1, y X2 y X las incógnitas.

Luego de identificados los coeficientes que acompañan a las incógnitas, se aplica la fórmula general para obtener las raíces, denominada resolvente. Es importante destacar que la aplicación de esta fórmula siempre arroja dos resultados dado el símbolo ±. Al sustituir las letras por los números, la resolvente quedaría de la siguiente manera:

Fórmula de la resolvente:

$x=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}$

Se sustituyen los valores de los coeficientes:

$x=\frac{-4\pm \sqrt{\left ( 4 \right )^{2}-4\left ( 3 \right )\left ( 1 \right )}}{2\left ( 3 \right )}$

Se resuelve lo que está dentro de la raíz cuadrada.

$x=\frac{-4\pm \sqrt{16-12}}{6} = \frac{-4\pm \sqrt{4}}{6}$

Se separa la ecuación en dos, uno con el signo positivo y otra con el signo negativo.

$x_{1}=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a} = \frac{-4+2}{6}=-\frac{1}{3}$

$x_{2}=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a} = \frac{-4-2}{6}=-1$

Un error recurrente durante la sustitución de las letras, es que se obvia el signo que acompaña a cada uno de los coeficientes, cambiando con ello los resultados de las incógnitas. Por ello, es importante incluir el símbolo positivo o negativo.

Incompletas

Son aquellas en las que al menos uno de los términos no cuadráticos tiene coeficiente cero. A diferencia de las ecuaciones completas, las incompletas se subdividen en dos tipos de ecuaciones: por una parte, están las que carecen del término lineal y las que carecen del término independiente.

En función de ello, se ejemplifican cada uno de los tipos de ecuaciones cuadráticas incompletas:

Ecuación de segundo grado incompleta sin el término lineal:

$ax^{2}+c=0$

Ejemplo:

$3x^{2}+2=0$

$3x^{2}=-2$

$x^{2}=-\frac{2}{3}$

$x^{2}=\sqrt{-\frac{2}{3}}$

En este caso, al ser despejada la incógnita y al aplicar raíz cuadrada, el valor de la incógnita no puede ser hallado debido a que no existe la raíz cuadrada de un número negativo. Por lo tanto, se concluye el ejercicio indicando que el número es imaginario.

Aunque en este caso, esta ecuación sólo posee dos coeficientes, a saber: a = +3 y c = +2, se sustituye la variable restante por un cero, resultando, b=0.

Ecuación de segundo grado incompleta sin el término independiente:

$ax^{2}-bx=0$

Ejemplo:

$x^{2}-2x=0$

Donde a=1; b=2; c=0

$x=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}$

$x=\frac{-2\pm \sqrt{2^{2}-4\left ( 1 \right )\left ( 0 \right )}}{2\left ( 1 \right )} = \frac{-2\pm \sqrt{4-4\left ( 0 \right )}}{2} = \frac{-2\pm \sqrt{4}}{2} = \frac{-2\pm 2}{2}$

$x_{1}=-\frac{4}{2} = -2$

$x_{2}=\frac{0}{2} = 0$

Resolución de las ecuaciones de segundo grado

Para ilustrar lo indicado anteriormente, se realizan algunos ejemplos de ecuaciones de segundo grado de manera tal que se identifique la forma de resolver.

Lo primero, es identificar esta ecuación en particular con la incógnita, que generalmente es representada con la letra equis y es elevada al cuadrado (x2). Posteriormente, se utiliza una fórmula denominada resolvente, que facilita la resolución de ecuación de segundo grado, en la cual se obtendrán siempre dos valores:

$x=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}$

Usando el ejemplo anterior sobre problemas de ecuaciones de segundo grado, podemos sustituir los números en la fórmula para hallar los dos valores de X, donde:

$3x^{2}-4x+1=0$

Donde a=3, b= -4, c=+1

$x=\frac{-\left ( -4 \right )\pm \sqrt{\left ( -4 \right )^{2}-4\left ( 3 \right )\left ( 1 \right )}}{2\left ( 3 \right )} = \frac{+4 \pm \sqrt{16-12}}{6} = \frac{+4 \pm \sqrt{4}}{6}$

$x_{1}=\frac{+4+2}{6} = \frac{6}{6} = 1$

$x_{2}=\frac{+4-2}{6} = \frac{2}{6} = \frac{1}{3}$

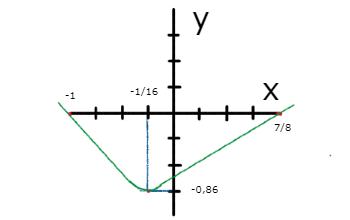
Ejemplo 1: Hallar la ecuación cuadrática cuyas raíces son -1 y 7/8. Graficar y determinar las coordenadas “x” y “x” del vértice.
- Paso 1: se realiza un producto notable con las raíces y se iguala a cero (0). Para crear se cambia el signo:
  (x+1)(x-7/8)=0
- Paso 2: se desarrollar el producto notable
  $x^{2}+\frac{7}{8}x+x-\frac{7}{8}=0$
  
  $x^{2}+\frac{1}{8}x+x-\frac{7}{8}=0$
- Paso 3: Para hallar la coordenada “x” del vértice se aplica la siguiente fórmula
  $V_{x}=\frac{ra+rb}{2}$
  
  $V_{x}=\frac{\frac{7}{8}+\left (-1 \right )}{2} = -\frac{1}{16}$
- Paso 4: Para hallar la coordenada “y” del vértice se sustituye la coordenada “x” en la ecuación cuadrática
  $V_{y}=\left ( \frac{1}{16} \right )^{2}+\frac{1}{8}\left ( \frac{1}{16} \right )-\frac{7}{8}$
  
  $V_{y}=-\frac{221}{256}\approx -0,86$
- Paso 5: Para la gráfica, escoger una escala con la que se visualicen los datos
Se requiere calcular los lados del triángulo que se muestra en la figura. Se debe tomar en cuenta que el triángulo es rectángulo y la hipotenusa tiene como valor 10 u.
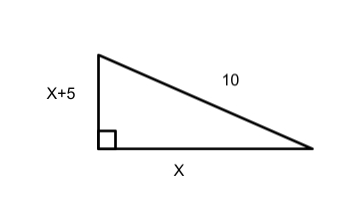
- Paso 1: se aplica el teorema de Pitágoras para crear a ecuación cuadrática
  $h^{2}=Co^{2}+Ca^{2}$
  $\left (10 \right )^{2}=\left (x+5 \right )^{2}+X^{2}$
  
  $100=X^{2}+10X+25+X^{2}$
  
  $2X^{2}+10X+75=0$
- Paso 2: se aplica la ecuación resolvente
  $x=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}$
  $x=\frac{-\left (10 \right )\pm \sqrt{10^{2}-4\left (2 \right )\left (-75 \right )}}{2\left (2 \right )} = \frac{-10\pm \sqrt{700}}{4}$
  
  $x_{1}=\frac{-10+\sqrt{700}}{4}\approx 4.11$
  
  $x_{2}=\frac{-10-\sqrt{700}}{4}\approx -9.114$
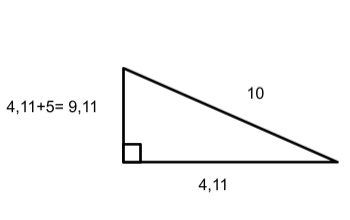
- Paso 3: se escoge la raíz positiva dado que se está hablando de una medida de longitud y no puede ser negativa
10 ejercicios con ecuaciones de segundo grado

A continuación, se presentan ejercicios resueltos de ecuaciones de segundo grado.
- Ejemplo 1:
  $2X^{2}+9X+10=0$
  
  Se deduce que es una ecuación completa, cuyos coeficientes son: a = +2, b = 9 y c = +10. Se sustituyen en la ecuación resolvente.
  
  $x=\frac{-9\pm \sqrt{\left (9 \right )^{2}-4\left ( 2 \right )\left ( 10 \right )}}{2\left ( 2 \right )}$
  
  Se resuelve el interior de la raíz cuadrada.
  
  $x=\frac{-9\pm \sqrt{81-80}}{4} = \frac{-9\pm \sqrt{1}}{4} = \frac{-9\pm 1}{4}$
  
  Se separa la ecuación en dos. Uno con el signo + y otra con el signo –
  
  $x_{1}=-\frac{8}{4} = -2$
  
  $x_{2}=-\frac{10}{4} = -\frac{5}{2}$
- Ejemplo 2:
  $3X^{2}-5X+2=0$
  $x=\frac{-\left ( -5 \right )\pm \sqrt{\left ( -5 \right )^{2}-4\left ( 3 \right )\left ( 2 \right )}}{2\left ( 3 \right )} = \frac{5\pm \sqrt{25-24}}{6} = \frac{5\pm \sqrt{1}}{6} = \frac{5\pm 1}{6}$
  
  $x_{1}=\frac{6}{6}=1$
  
  $x_{2}=\frac{4}{6}=\frac{2}{3}$
- Ejemplo 3:
  $3X^{2}-4X+1=0$
  $x=\frac{-\left ( -4 \right )\pm \sqrt{\left ( -4 \right )^{2}-4\left ( 3 \right )\left ( 1 \right )}}{2\left ( 3 \right )} =\frac{4\pm \sqrt{16-12}}{6} = \frac{4\pm \sqrt{4}}{6} = \frac{4\pm 2}{6}$
  
  $x_{1} = \frac{4+ 2}{6} = \frac{6}{6} = 1$
  
  $x_{2} = \frac{4- 2}{6} = \frac{2}{6} = \frac{1}{3}$
- Ejemplo 4:
  $3X^{2}-4X+1=0$
  $x=\frac{-\left ( -4 \right )\pm \sqrt{\left ( -4 \right )^{2}-4\left ( 3 \right )\left ( 1 \right )}}{2\left ( 3 \right )} = \frac{+4\pm \sqrt{16-12}}{6} = \frac{+4\pm \sqrt{4}}{6} = \frac{+4\pm 2}{6}$
  
  $x_{1}=\frac{+4+ 2}{6} = \frac{6}{6} = 1$
  
  $x_{2}=\frac{+4- 2}{6} = \frac{2}{6} = \frac{1}{3}$
- Ejemplo 5:
  $X^{2}+X+1=0$
  $x=\frac{-1\pm \sqrt{1^{2}-4\left (1 \right )\left (1 \right )}}{2\left (1 \right )} = \frac{-1\pm \sqrt{1-4}}{2} = \frac{-1\pm \sqrt{-3}}{2} = \frac{-1\pm i\sqrt{3}}{2}$
  
  $x_{1} = \frac{-1+ i\sqrt{3}}{2}$
  
  $x_{2} = \frac{-1- i\sqrt{3}}{2}$
- Ejemplo 6:
  $X^{2}+3X+2=0$
  $x=\frac{-3\pm \sqrt{3^{2}-4\left ( 1 \right )\left ( 2 \right )}}{2\left ( 1 \right )} = \frac{-3\pm \sqrt{9-8}}{2} = \frac{-3\pm \sqrt{1}}{2} = \frac{-3\pm 1}{2}$
  
  $x_{1} = \frac{-3+ 1}{2} = \frac{-2}{2} = -1$
  
  $x_{2} = \frac{-3- 1}{2} = \frac{-4}{2} = -2$
- Ejemplo 7:
  $5X^{2}+20X+15=0$
  $x=\frac{-\left ( -20 \right )\pm \sqrt{\left ( -20 \right )^{2}-4\left ( 5 \right )\left ( 15 \right )}}{2\left ( 5 \right )} = \frac{20\pm \sqrt{400-300}}{10} = \frac{20\pm \sqrt{100}}{10} = \frac{20\pm 10}{10}$
  
  $x_{1}=\frac{20+10}{10} = \frac{30}{10} = 3$
  
  $x_{2}=\frac{20-10}{10} = \frac{20}{10} = 2$
- Ejemplo 8:
  $X^{2}+1=0$
  $X^{2}= -1$
  
  $X=\pm \sqrt{-1} = \pm i$
- Ejemplo 9:
  $1-3X\left ( 1-X \right )=0$
  $1-3X+3X^{2}=0$
  
  $3X^{2}-3X+1=0$
  
  $x=\frac{-\left ( -3 \right )\pm \sqrt{\left ( -3 \right )^{2}-4\left ( 3 \right )\left ( 1 \right )}}{2\left ( 3 \right )} = \frac{3\pm \sqrt{9-12}}{6} = \frac{3\pm \sqrt{-3}}{6} = \frac{3\pm i\sqrt{3}}{6} = \frac{3}{6}\pm \frac{i\sqrt{3}}{6}$
  
  $x_{1}=\frac{1}{2}+ \frac{i\sqrt{3}}{6}$
  
  $x_{2}=\frac{1}{2}- \frac{i\sqrt{3}}{6}$
- Ejemplo 10:
  $2X^{2}+1=X^{2}+2$
  $2X^{2}-X^{2}=2-1$
  
  $X^{2}=1$
  
  $X=\sqrt{1}$
  
  $X=\pm 1$
- Determinar la ecuación cuadrática de la parábola cuyo vértice se encuentra en el punto (4,20) y una de sus raíces es -2.
  - Paso 1: Para hallar las raíces se hace uso de la ecuación para determinar la coordenada x del vértice.
    $V_{x}=\frac{ra+rb}{2}$
    Donde Vx = 4
    $4=\frac{ra+\left (-2 \right )}{2}$
    Se despeja ra
    $8=ra-2$
    $ra=10$
  - Paso 2: Ya determinadas ambas raíces, se crea un producto notable. Se cambia el signo.
    $\left ( x+2 \right )\left ( x-10 \right )=0$
    Se desarrolla el producto notable
    $x^{2}-10x+2x-20=0$
    $x^{2}-8x-20=0$
- Se requiere calcular los lados del triángulo que se muestra en la figura. Se debe tomar en cuenta que el triángulo es rectángulo y la hipotenusa tiene como valor 10 u.
  - Paso 1: se aplica el teorema de Pitágoras para crear a ecuación cuadrática
    $h^{2}=Co^{2}+Ca^{2}$
    $\left (10 \right )^{2}=\left (x+5 \right )^{2}+X^{2}$
    
    $100=X^{2}+10X+25+X^{2}$
    
    $2X^{2}+10X+75=0$
  - Paso 2: se aplica la ecuación resolvente
    $x=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}$
    $x=\frac{-\left (10 \right )\pm \sqrt{10^{2}-4\left (2 \right )\left (-75 \right )}}{2\left (2 \right )} = \frac{-10\pm \sqrt{700}}{4}$
    
    $x_{1}=\frac{-10+\sqrt{700}}{4}\approx 4.11$
    
    $x_{2}=\frac{-10-\sqrt{700}}{4}\approx -9.114$
  - Paso 3: se escoge la raíz positiva dado que se está hablando de una medida de longitud y no puede ser negativa
  10 ejercicios con ecuaciones de segundo grado
  
  A continuación, se presentan ejercicios resueltos de ecuaciones de segundo grado.
  - Ejemplo 1:
    $2X^{2}+9X+10=0$
    
    Se deduce que es una ecuación completa, cuyos coeficientes son: a = +2, b = 9 y c = +10. Se sustituyen en la ecuación resolvente.
    
    $x=\frac{-9\pm \sqrt{\left (9 \right )^{2}-4\left ( 2 \right )\left ( 10 \right )}}{2\left ( 2 \right )}$
    
    Se resuelve el interior de la raíz cuadrada.
    
    $x=\frac{-9\pm \sqrt{81-80}}{4} = \frac{-9\pm \sqrt{1}}{4} = \frac{-9\pm 1}{4}$
    
    Se separa la ecuación en dos. Uno con el signo + y otra con el signo –
    
    $x_{1}=-\frac{8}{4} = -2$
    
    $x_{2}=-\frac{10}{4} = -\frac{5}{2}$
  - Ejemplo 2:
    $3X^{2}-5X+2=0$
    $x=\frac{-\left ( -5 \right )\pm \sqrt{\left ( -5 \right )^{2}-4\left ( 3 \right )\left ( 2 \right )}}{2\left ( 3 \right )} = \frac{5\pm \sqrt{25-24}}{6} = \frac{5\pm \sqrt{1}}{6} = \frac{5\pm 1}{6}$
    
    $x_{1}=\frac{6}{6}=1$
    
    $x_{2}=\frac{4}{6}=\frac{2}{3}$
  - Ejemplo 3:
    $3X^{2}-4X+1=0$
    $x=\frac{-\left ( -4 \right )\pm \sqrt{\left ( -4 \right )^{2}-4\left ( 3 \right )\left ( 1 \right )}}{2\left ( 3 \right )} =\frac{4\pm \sqrt{16-12}}{6} = \frac{4\pm \sqrt{4}}{6} = \frac{4\pm 2}{6}$
    
    $x_{1} = \frac{4+ 2}{6} = \frac{6}{6} = 1$
    
    $x_{2} = \frac{4- 2}{6} = \frac{2}{6} = \frac{1}{3}$
  - Ejemplo 4:
    $3X^{2}-4X+1=0$
    $x=\frac{-\left ( -4 \right )\pm \sqrt{\left ( -4 \right )^{2}-4\left ( 3 \right )\left ( 1 \right )}}{2\left ( 3 \right )} = \frac{+4\pm \sqrt{16-12}}{6} = \frac{+4\pm \sqrt{4}}{6} = \frac{+4\pm 2}{6}$
    
    $x_{1}=\frac{+4+ 2}{6} = \frac{6}{6} = 1$
    
    $x_{2}=\frac{+4- 2}{6} = \frac{2}{6} = \frac{1}{3}$
  - Ejemplo 5:
    $X^{2}+X+1=0$
    $x=\frac{-1\pm \sqrt{1^{2}-4\left (1 \right )\left (1 \right )}}{2\left (1 \right )} = \frac{-1\pm \sqrt{1-4}}{2} = \frac{-1\pm \sqrt{-3}}{2} = \frac{-1\pm i\sqrt{3}}{2}$
    
    $x_{1} = \frac{-1+ i\sqrt{3}}{2}$
    
    $x_{2} = \frac{-1- i\sqrt{3}}{2}$
  - Ejemplo 6:
    $X^{2}+3X+2=0$
    $x=\frac{-3\pm \sqrt{3^{2}-4\left ( 1 \right )\left ( 2 \right )}}{2\left ( 1 \right )} = \frac{-3\pm \sqrt{9-8}}{2} = \frac{-3\pm \sqrt{1}}{2} = \frac{-3\pm 1}{2}$
    
    $x_{1} = \frac{-3+ 1}{2} = \frac{-2}{2} = -1$
    
    $x_{2} = \frac{-3- 1}{2} = \frac{-4}{2} = -2$
  - Ejemplo 7:
    $5X^{2}+20X+15=0$
    $x=\frac{-\left ( -20 \right )\pm \sqrt{\left ( -20 \right )^{2}-4\left ( 5 \right )\left ( 15 \right )}}{2\left ( 5 \right )} = \frac{20\pm \sqrt{400-300}}{10} = \frac{20\pm \sqrt{100}}{10} = \frac{20\pm 10}{10}$
    
    $x_{1}=\frac{20+10}{10} = \frac{30}{10} = 3$
    
    $x_{2}=\frac{20-10}{10} = \frac{20}{10} = 2$
  - Ejemplo 8:
    $X^{2}+1=0$
    $X^{2}= -1$
    
    $X=\pm \sqrt{-1} = \pm i$
  - Ejemplo 9:
    $1-3X\left ( 1-X \right )=0$
    $1-3X+3X^{2}=0$
    
    $3X^{2}-3X+1=0$
    
    $x=\frac{-\left ( -3 \right )\pm \sqrt{\left ( -3 \right )^{2}-4\left ( 3 \right )\left ( 1 \right )}}{2\left ( 3 \right )} = \frac{3\pm \sqrt{9-12}}{6} = \frac{3\pm \sqrt{-3}}{6} = \frac{3\pm i\sqrt{3}}{6} = \frac{3}{6}\pm \frac{i\sqrt{3}}{6}$
    
    $x_{1}=\frac{1}{2}+ \frac{i\sqrt{3}}{6}$
    
    $x_{2}=\frac{1}{2}- \frac{i\sqrt{3}}{6}$
  - Ejemplo 10:
    $2X^{2}+1=X^{2}+2$
    $2X^{2}-X^{2}=2-1$
    
    $X^{2}=1$
    
    $X=\sqrt{1}$
    
    $X=\pm 1$

Preguntas Frecuentes sobre las Ecuaciones de Segundo Grado

Es una suma algebraica igualada a cero y compuesta por tres términos: una incógnita elevada al cuadrado, una incógnita elevada al uno y un término independiente.
2X²+9X+10=0 Leer más

Se puede crear a través de un polinomio de segundo grado con o sin término lineal e independiente. El polinomio debe ser igualado a cero.
También se puede generar a través de un producto notable, a través del cálculo integral de una ecuación lineal y por medio de la multiplicación de una ecuación lineal por su variable.
Se recomienda el uso de un producto notable donde escojan números enteros para tener la certeza de obtener raíces reales. Leer más

Verificar que tenga un término cuadrático e identificar qué tipo de ecuación es (completa o incompleta).
En caso de que sea completa, identificar las letras a, b y c; donde a, es la variable que acompaña a la incógnita al cuadrado, b es la variable que acompaña la incógnita con exponente a la 1 y c es la variable independiente.
aX²+bX+c=0
Aplicar la siguiente fórmula y sustituir los valores que acompañan a las incógnitas
$x=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}$
Despejar la equis. Al hacerlo, se generarán dos resultados debido a que la fórmula tiene un símbolo de ±. El valor que genere la raíz cuadrada se resta y luego se suma por separado.
En caso de que sea incompleta, existen varias formas de hallar el valor de la incógnita: o se aplica la resolvente y se sustituye el término faltante por un cero, o se aplica un procedimiento distinto

Es necesario haber enseñado previamente las siguientes operaciones matemáticas:

Calcular la raíz cuadrada.
Hallar el producto notable.
Identificar el factor común.
Realizar la factorización.

Una vez aprendidas, es necesario identificar qué tipo de ecuación es, y aplicar los diferentes métodos de resolución, según el tipo de ecuación cuadrática, salvo que existan casos especiales.
Leer más

Existen dos tipos de ecuaciones incompletas: las que no poseen el término lineal y las que no poseen el término independiente.
CASO 1:aX²+c =0
CASO 2:aX²+bX=0
En cualquier caso, se debe aplicar la fórmula de la resolvente $x=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}$ y sustituir los coeficientes faltantes por ceros. Leer más

Expresiones Algebraicas

Números Reales

Ecuaciones de Primer Grado

Bibliografía

Materano, Eli . ( Última edición: 22 de junio de 2023 a las 11:06 am). Definición de Ecuaciones de Segundo Grado. Recuperado de: https://conceptodefinicion.de/ecuaciones-de-segundo-grado/. Consultado el 26 de marzo de 2024

Ecuaciones de Segundo Grado

Qué son las ecuaciones de segundo grado

Qué son las ecuaciones de segundo grado

Características de las ecuaciones de segundo grado

Fórmula de las ecuaciones de segundo grado

Clasificación

Completas

Incompletas

Resolución de las ecuaciones de segundo grado

10 ejercicios con ecuaciones de segundo grado

10 ejercicios con ecuaciones de segundo grado

Preguntas Frecuentes sobre las Ecuaciones de Segundo Grado

¿Qué es una ecuación de segundo grado?

¿Cómo hacer ecuaciones de segundo grado?

¿Cómo se resuelven las ecuaciones de segundo grado?

¿Cómo enseñar ecuaciones de segundo grado?

¿Cómo resolver ecuaciones de segundo grado incompletas?

Expresiones Algebraicas

Números Reales

Ecuaciones de Primer Grado

Bibliografía

Comparte este artículo