Qué son los números decimales
Corresponde a la expresión de números no enteros, los cuales se encargan de denotar tanto números racionales, como irracionales. Están compuestos por una parte entera y otra parte decimal diferente al número 0.
Desde el punto de vista etimológico, proviene de la palabra de origen latín “decimus” que significa décimo.
Características de los números decimales
Entre las principales propiedades de estos números se encuentran:
- Su valor no se altera si un cero es añadido o suprimido a su derecha. Es decir, es lo mismo 0,48 que 0,480 o 0,4800.
- Si el punto se corre hacia la derecha el resultado será igual a la multiplicación del número decimal inicial por la unidad (1) seguido de tantos ceros como posiciones se haya corrido el punto. Por ejemplo, si al número 8.347 se le corre el punto a la derecha dos puestos el resultado sería 834.7, lo que es igual a 8.347 x 100.
- Por el contrario, si el punto se corre hacia la izquierda el resultado será igual al número decimal inicial entre la unidad (1) seguida de tantos ceros como posiciones se corre el punto.
- Todos los números decimales tienen un sucesor y este puede ser cualquier número.
- Para representar los números decimales en una recta numérica, se deben tomar dos números de la escala entre los cuales está comprendido el número decimal y dentro de este tramo se divide en 10 partes que vendrían siendo las décimas.
Lectura y escritura de números decimales

En la mayoría de los casos la escritura de números decimales se realiza haciendo uso de un punto (.) para separar la parte entera de la parte decimal, sin embargo, en algunas literaturas utilizan una coma (,) o un apóstrofe ( ´) para separarlos, expresando de manera escrita los números decimales. Ejemplo:
- 2.49
- 2,49
- 2´49
En cuanto a la lectura de números decimales, existen dos formas para leerlos, la primera es decir el número entero, luego el punto y posteriormente nombrar los números decimales de manera individual, la segunda forma es parecida, solo que la porción decimal se agrupa y se dice la cifra completa. Ejemplo con el número 8.234:
- Ocho punto dos tres cuatro.
- Ocho punto doscientos treinta y cuatro.
Otras formas de lectura de números decimales serían las siguientes:
- Ocho con doscientos treinta y cuatro.
- Ocho unidades y doscientos treinta y cuatro centésimas.
Clasificación de los números decimales
Estos se clasifican de la siguiente manera:
Exactos
Estos son aquellos en los que la porción decimal está conformada por una cifra numérica finita, por ejemplo, 4.8 o 2.98…
Periódicos
Son todos aquellos que poseen una cifra decimal ilimitada, es decir que los números de la parte decimal se repiten infinitamente. Estos pueden ser de dos tipos:
Puros
Son aquellos cuya parte decimal es única y periódica, como es el caso de 4.9999999999…
Mixtos
La parte decimal está compuesta en inicio por una porción no periódica, seguida de una periódica infinita, por ejemplo 8.983333333333.
No periódicos
Son denominados como no exactos y no periódicos y en este caso la cifra decimal es infinita pero no se repite, un ejemplo sería 4.84939483483…
Conversión de números decimales
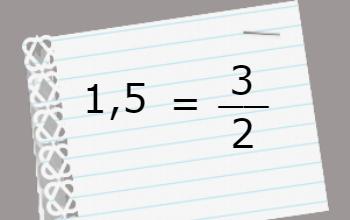
Estos números se encuentran relacionados con las fracciones, por lo tanto, es común que se realicen procedimientos de conversión entre ellos.
Decimales a fracciones
Para pasar un numero de decimal a fracción se deben seguir los siguientes pasos:
- Hacer una fracción en la cual el numerador será el número decimal y el denominador estará representado por el número uno.
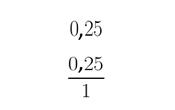
- En segundo lugar, se debe ubicar una fracción equivalente. En esta nueva fracción el denominador estará comprendido por la unidad (1) seguido de tantos ceros como decimales tenga el número.
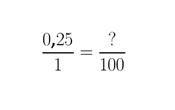
- Multiplicar el número decimal, es decir, el numerador por ese número ubicado como denominador en la fracción equivalente.
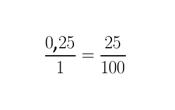
- Por último, se simplifica la fracción.
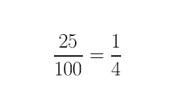
Fracciones a decimales
En muchas ocasiones es necesario pasar un número de fracción a decimal, una de estas es para lograr representarlo en una recta numérica con decimales. Para este procedimiento existen tres formas posibles:
- Por medio de una división.
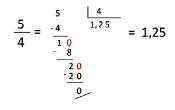
- Con una fracción de denominador 10, 100… Se rueda el punto en el numerador hacia la izquierda tantas veces como 0 posea el denominador.

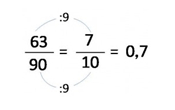
- Con una fracción equivalente. Esto puede ser por medio de multiplicación (amplificación) o división (simplificación) tanto del numerador como del denominador por el mismo número, siempre y cuando el resultado corresponda con una fracción cuyo denominador sea igual a 10, 100, 1000…
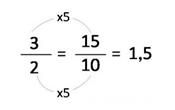
Operaciones con números decimales
A continuación, se presentan ejercicios resueltos de operaciones matemáticas con números decimales.
- Un número decimal entre uno entero:
- Se divide como si de dos números enteros se tratase.
- Al bajar y dividir el primer número decimal, se agrega una coma en el cociente.
- Un número entero entre uno decimal:
- Ya que no se puede realizar la división con un divisor decimal, este se debe transformar en número entero.
- Para lograr esta transformación se debe multiplicar el número divisor por la unidad (1) seguida de tantos ceros como decimales requieran ser eliminados.
- El dividendo también debe ser multiplicado por el mismo número por el cual se multiplicó el divisor.
- Se obtiene una división de números enteros.
- El resto o resultado se debe dividir por el mismo número por el que fueron multiplicados el divisor y el dividendo para obtener el resultado final.
- División de dos números decimales:
- Ambos, tanto divisor como dividendo se multiplican por la unidad (1) seguida de tantos ceros como decimales se quieran eliminar en el divisor.
- Una vez obtenidos los números enteros se procede a dividir.
- El resto o resultado se debe dividir por el mismo número por el que fueron multiplicados el divisor y el dividendo para obtener el resultado final.