Qué es probabilidad
Es la posibilidad de que un evento suceda dependiendo de las condiciones dadas para que acontezca (ejemplo: qué probabilidad hay de que llueva). Será medida entre 0 y 1 o expresada en porcentajes, dichos rangos podrán observarse en ejercicios resueltos de probabilidad. Para ello se medirá la relación entre los sucesos favorables y los posibles.
Los sucesos favorables son los válidos según la experiencia del individuo; y los posibles son los que pueden darse si son válidos o no a su experiencia. La probabilidad y estadística están relacionadas al ser el área donde se registran sucesos. La etimología del término viene del latín probabilitas o posibilitatis, relacionadas a “probar” o “comprobar” y tat que se refiere a “cualidad”. El término se relaciona a la cualidad de probar.
Historia de la probabilidad
Siempre ha estado en la mente del hombre, cuando observaban la posibilidad de algún hecho, por ejemplo, la diversidad en los estados del clima basado en la observación de fenómenos naturales para determinar cuál posible escenario climático pudiese acontecer.
Los sumerios, egipcios y romanos utilizaron el astrágalo (hueso del talón) de algunos animales, para tallarlos de tal forma que al ser lanzados pudiesen caer en cuatro posibles posiciones y qué probabilidad hay de que caiga en una u otra (como los actuales dados). Se encontraron tablas donde presuntamente realizaban anotaciones de resultados.
Hacia 1660 salió a la luz un texto sobre los primeros fundamentos del azar escrito por el matemático Gerolamo Cardano (1501-1576) y en el siglo XVII los matemáticos Pierre Fermat (1607-1665) y Blaise Pascal (1623-1662) intentaron solventar problemas sobre juegos de azar.
Basado en sus aportes, el matemático Christiaan Huygens (1629-1695) intentó explicar las probabilidades sobre ganar un juego y publicó sobre la probabilidad.
Surgieron luego aportes como el teorema de Bernoulli, teorema del límite y la de errores y la teoría de probabilidades, centrándose en ello Pierre-Simon Laplace (1749-1827) y Carl Frierich Gauss (1777-1855).
El naturalista Gregor Mendel (1822-1884) la aplicó para la ciencia, estudiando la genética y posibles resultados en la combinación de genes específicos. Finalmente, el matemático Andrei Kolmogorov (1903-1987) en el siglo XX inició la teoría de la probabilidad que se conoce en la actualidad (teoría de la medida) y se utiliza la estadística probabilidad.
Medición de la probabilidad
Regla de la adición
Si se tienen un suceso A y uno B, su cálculo sería expresado con la siguiente fórmula:
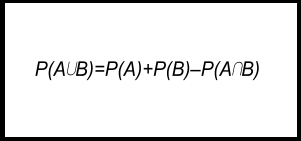
tomando en cuenta que P(A) corresponde a la posibilidad del suceso A; P(B) sería la posibilidad del suceso B.

Esta expresión significa la posibilidad que ocurra cualquiera.
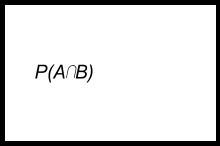
Esta expresión representa la posibilidad que ocurran ambos simultáneamente.
Su excepción es si los sucesos son excluyentes entre sí (no pueden ocurrir al mismo tiempo) por no poseer elementos en común. Un ejemplo sería la probabilidad de lluvia, las dos posibilidades serían que lloviera o no, pero no pueden darse ambas condiciones a la vez.
Con la fórmula:

Regla de la multiplicación
Tanto un suceso A como uno B ocurren simultáneamente (probabilidad conjunta), pero está sujeta a determinar si ambos eventos son independientes o dependientes. Serán dependientes cuando la existencia de uno influye en la existencia del otro; e independientes si no tienen conexión (la existencia de uno no tiene que ver con que el otro ocurra). Se determina por:
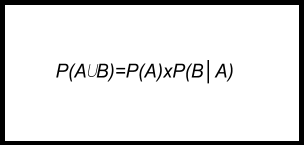
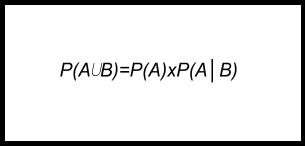
Ejemplo: se lanza una moneda al aire dos veces, y la posibilidad de que salga la misma cara sería determinado por:
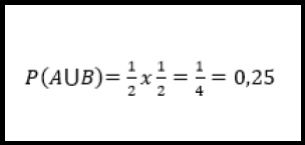
por lo que existe un 25% de posibilidad que la misma cara salga ambas veces.
Regla Laplace
Sirve para realizar estimaciones sobre las posibilidades de un suceso que no es muy frecuente.
Determinada por:

Ejemplo: hallar el porcentaje de posibilidad de sacar un As de un mazo de cartas de 52 piezas. En este caso, los casos posibles son 52 mientras que los casos favorables 4:
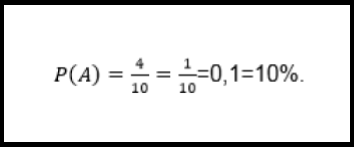
Distribución binomial
Se trata de una distribución de probabilidad donde sólo se obtienen dos resultados posibles, conocidos como éxito y fracaso. Debe cumplir con: su posibilidad de éxito y fracaso debe ser constante, cada resultado es independiente, no pueden ocurrir los dos simultáneamente. Su fórmula es
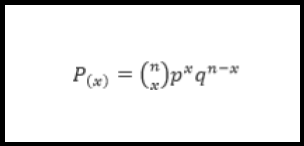
donde n es el número de intentos, x los éxitos, p probabilidades de éxito y q probabilidades de fracaso (1-p), también donde
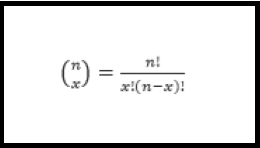
Ejemplo: si en un salón el 75% de los estudiantes estudiaron para el examen final, luego 5 de ellos se reúnen. ¿Cuál es la probabilidad que 3 de ellos hayan aprobado?
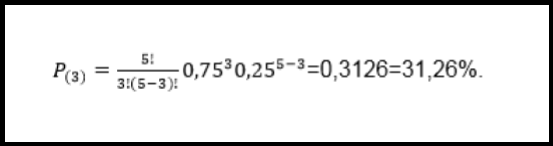
Tipos de probabilidad

Probabilidad clásica
Todos los casos posibles tienen la misma posibilidad de suceder. Un ejemplo es una moneda, en el que las posibilidades son las mismas que salga cara o sello.
Probabilidad condicionada
Es la probabilidad que un suceso A ocurra en conocimiento que también sucede otro B y se expresa P(A|B) o P(B|A) según sea el caso y se entendería como “la probabilidad de B dado A”. No existe necesariamente relación entre ambos o puede que uno sea consecuencia del otro, e incluso pueden suceder al mismo tiempo. Su fórmula está dada por
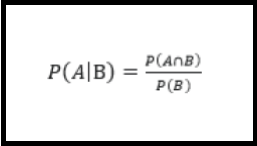
Ejemplo: en un grupo de amigos al 30% les gusta la montaña y la playa, y al 55% les gusta la playa, ¿Cuál sería la probabilidad que a uno que le guste la playa, le guste la montaña? Los sucesos serían que a uno le guste la montaña [P(A)=?], a otro le guste la playa [P(B)=55%] y que le guste la montaña y la playa [P(AB)=30%], por lo que:
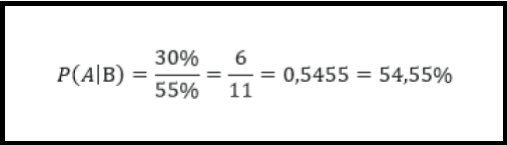
Probabilidad frecuencial
Se dividen los casos favorables con los posibles, cuando estos últimos tiende a infinito. Su fórmula es
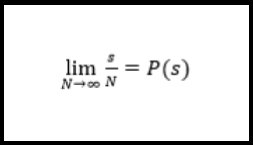
siendo s es el suceso, N la cantidad de casos y P(s) la probabilidad del evento.
Aplicaciones de la probabilidad
Su aplicación resulta útil en diversas áreas y ciencias. Por ejemplo, la probabilidad y estadística mantienen una estrecha relación, así como con la matemática, la física, la contaduría, la filosofía, entre otras, en las que su teoría ayuda a llegar a conclusiones sobre eventualidades posibles y encontrar los métodos de combinar los eventos cuando intervienen varios sucesos en un experimento aleatorio o prueba.
Un ejemplo palpable es la predicción de los estados del tiempo, juegos de azar, proyecciones económicas o geopolíticas, probabilidad de daño que toma en cuenta una empresa de seguros, entre otras.