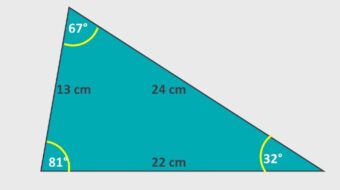
Un Triángulo debe cumplir con ciertas propiedades para ser considerado como tal. algunas de ellas son las siguientes:
- La suma de los ángulos interiores de un triángulo es igual a 180 °.
- Cada triángulo equilátero es equiangular, es decir, las medidas de sus ángulos internos son iguales, en este caso cada ángulo mide 60 °
- Si dos lados de un triángulo tienen la misma medida, entonces los ángulos opuestos también son de igual medida.
- En un triángulo, un mayor lado se opone a un mayor ángulo.
- El valor de un ángulo exterior de un triángulo es igual a la suma de los dos interiores no adyacentes.
- Un lado de un triángulo es más pequeño que la suma de los otros dos y mayor que su diferencia. a (b + c a b) – c
Un triángulo muy utilizado en trigonometría es el triángulo rectángulo, en el cual el estudio de la relación entre sus lados está hecho por el teorema de Pitágoras.
Teorema de Pitágoras: Pitágoras enunció el famoso teorema que lleva su nombre y que relaciona los lados de un triángulo rectángulo. Este teorema dice:
“El área del cuadrado construida sobre la hipotenusa de un triángulo rectángulo es igual a la suma de las áreas de los cuadrados construidos en los catetos.”
Los triángulos son clasificados según dos criterios: según sus lados y según sus ángulos, éstos se pueden usar juntos o por separado:
1. Clasificación de triángulos según sus lados
- Un triángulo es equilátero, si tiene tres lados iguales.
- Un triángulo es isósceles, si tiene dos de sus lados iguales.
- Un triángulo es escaleno, si tiene sus tres lados desiguales.
2. Clasificación de triángulos según sus ángulos
En este caso, miramos los ángulos para realizar la clasificación. A saber:
- Un triángulo es agudo, si tiene todos sus ángulos agudos.
- Un triángulo es rectángulos, si tiene uno de sus ángulos rectos, es decir, 90º.
- Un triángulo es obtuso, si tiene un ángulo obtuso.