Qué es el triángulo escaleno
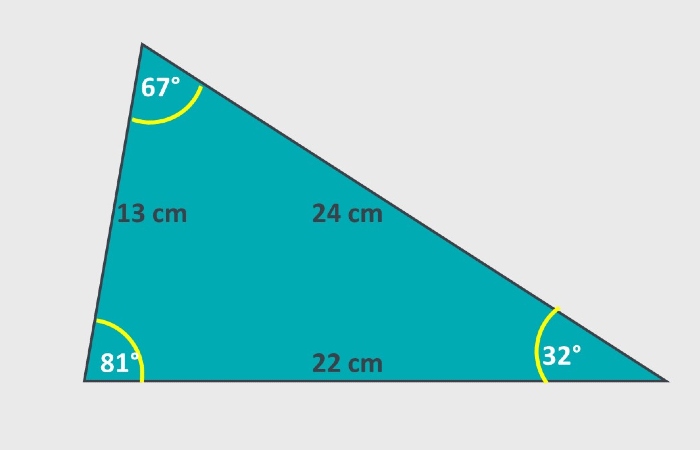
Es una figura geométrica que posee tres lados de diferentes longitudes y los tres ángulos tienen diferentes medidas. Los ángulos de este triángulo siguen la propiedad de la suma de ángulos y siempre suman 180°.
Las diferencias básicas entre los triángulos equilátero, isósceles y escaleno puede verse en la siguiente tabla:
| Dos lados poseen la misma longitud, cualquiera de ellos. | Los tres lados son de igual longitud. | Tres lados de longitudes desiguales. |
| Tienen dos ángulos iguales. | Sus tres ángulos miden 60 grados. | Tres ángulos de medidas diferentes. |
Este concepto se encuentra compuesto etimológicamente por dos palabras, triángulo, la cual deriva del latín triangulus y quiere decir tres ángulos, y por la palabra scalēnus que significa desigual.
Características del triángulo escaleno
Algunas de las propiedades importantes de este tipo de triángulos son las siguientes:
- No tiene lados iguales.
- No tiene ángulos iguales.
- No tiene eje de simetría.
- No tiene simetría puntual.
- Los ángulos dentro de este triángulo pueden ser un ángulo agudo, obtuso o recto.
- Si todos los ángulos del triángulo miden menos de 90 grados (agudo), entonces el centro del círculo que lo circunscribe estará dentro de un triángulo.
- En un triángulo obtuso escaleno, el circuncentro estará fuera del triángulo.
- Existen los triángulos escalenos rectángulos, obtusángulos y agudos.
Ecuaciones del triángulo escaleno
Las principales fórmulas del triángulo escaleno son las que se usan para calcular el área y el perímetro. De estas a su vez pueden calcularse otras partes como los lados, la base, la altura, entre otros.
Calcular área
El área de un triángulo escaleno se calcula mediante el uso de la siguiente fórmula:
Dónde:
- b: es la base.
- h: es la altura del triángulo escaleno.
Además, existen otras fórmulas que pueden utilizarse para calcular el área dependiendo de los datos que se tienen.
Si se conocen los tres lados:
Donde:
- a, b y c: son los lados del triángulo.
: es la mitad del perímetro, o semiperímetro.
Si se conoce un ángulo correspondiente y dos lados del triángulo:
Donde:
- a, b y c: son los lados del triángulo.
- A, B y C: son los ángulos del triángulo escaleno.
- sen: es el seno (función trigonométrica).
Ejemplo 1: si un triángulo escaleno tiene una altura de 5m y una base de 8m, ¿cuál sería el área del triángulo? Tiene una base de 8 m y una altura de 5 m.
Se tienen los datos:
- b = 8 m
- h = 5 m
Entonces,
Por lo tanto, el área del triángulo escaleno es
Ejemplo 2: calcular el área del triángulo escaleno si se conocen los tres lados del triángulo.
a = 6 cm.
b = 10 cm.
c = 8 cm.
Calcular perímetro
El perímetro del triángulo escaleno se obtiene al utilizar la fórmula:
Donde:
- a, b y c: son los lados del triángulo.
Ejemplo 1: En un triángulo escaleno de lados 5 m, 6 m y 7 m, ¿cuál es su perímetro?
Se tienen los siguientes datos:
- a = 5 m
- b = 6 m
- c = 7 m
Por lo tanto,
Entonces, el perímetro del triángulo escaleno es de 18 m.
- a, b y c: son los lados del triángulo.
Ejemplo 2: En un triángulo escaleno de lados 10 m, 15 m y 20 m, ¿cuál es su perímetro?
Se tienen los siguientes datos:
- a = 10 m
- b = 15 m
- c = 20 m
Por lo tanto,
Entonces, el perímetro del triángulo escaleno es de 45 m.
Ejemplos de triángulos escalenos
En la vida diaria son diversas las imágenes de triángulos escalenos que pueden ser observadas y que por lo general pasan desapercibidas. Entre los ejemplos más comunes se encuentran:
- Veleros.
- Rampas.
- Armaduras de techo.
- Grúas.